Свойства двухуровневых планов

При использовании двухуровневых полных и дробных факторных планов для построения полиномиальных моделей (без членов x₁²) они отвечают перечисленным ниже условиям.

1. Симметричность относительно центра плана:

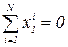, i=1,...,k.

2. Условие нормировки:

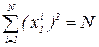
3. Ортогональность:

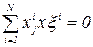j,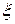=1,…,k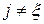

Если модель линейна, то ПФП и ДФП являются и ротатабельными и, соответственно, .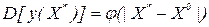

Если модель включает в себя эффекты взаимодействия, то план становится неротатабельным.

Следует заметить, что как ПФД, так и ДФП не позволяют выде­лить эффекты от функций вида x₁², I=1,...,k, поскольку для них со­ответствующий столбец в матрице F будет состоять из +1 так же, как и для коэффициентов Ь0. Это означает, что оценка коэффициента b₀ является смешанной оценкой для b₀ и b₁₁, i=1,....k, т.е.

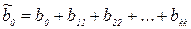, так как 1=x₁² = х₂² =...= x_k².

Используя это свойство, можно проверить значимость квадратич­ных эффектов. Для этого в центре плана Х⁰ проводится n₀ дополни­тельных опытов, и по их результатам вычисляются 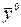и оценка дис­персии ошибки наблюдений :

;

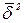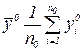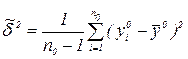
Если квадратичные эффекты отсутствуют, то оценк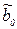и и 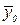долж­ны различаться незначимо. Для проверки этого используется гипоте­за Н₀: 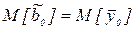. В качестве меры рассогласования может исполь­зоваться статистика вида

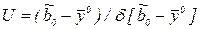. (6.1)

где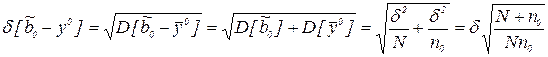

Поскольку значение 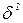неизвестно, то вместо нее используется оценка 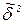найденная по наблюдениям в центре плана х₀ и распределённая по 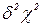-распределению с (n₀-1) степенями свободы.

Величина U распределена по t-распределению с (n₀-1) степенями свободы (по числу степеней свободы оценки 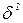). Если при заданном уровне значимости а выполняется условие U<U_Kp., то расхождения можно считать незначимыми. В противном случае они значимы и в мо­дель нужно вводить учет квадратичных эффектов.