Последовательный симплекс-метод

Лекция 15

Идея метода заключается в одновременном изучении поведения целевой функции и движении в пространстве варьируемых переменных. При этом движение осуществляется начиная с (n+1)-го опыта путём отражения наихудшей из последних n точек относительно "центра тяжести" оставшихся (n-1) точек,обеспечивая таким образом движение к более оптимальным значениям выходной переменной. После реализации опыта в новой точке процедуру отражения повторяют для новой совокупности из n точек и т.д. В результате образуется цепочка точек, перемещающихся к экстремуму целевой функции.

В качестве совокупности точек в k-мерном пространстве используется выпуклая фигура,образованная из (k+1) точек,не принадлежащих одновременно ни одному из (k-1)-мерных подпространств k-мерного исследуемого пространства. Эта фигура носит название симплекса. (Отсюда и название метода.) В 2-х мерном пространстве это треугольник,в 3-х мерном - любая треугольная пирамида (тетраэдр) и т.д.

Обычно в качестве начального используют регулярный симплекс, расстояние в котором между всеми вершинами (длина ребра) - одинаково.

При размещении центра симплекса в начале координат,а (k+1)-ой вершины на оси xk, остальные вершины будут располагаться симметрично относительно координатных осей в точках с координатами:

Номер	Координаты вершин
столбца	x1	x2	x3	...	xk-1	xk
	-r1	-r2	-r3	...	-rk-1	-rk
	R1	-r2	-r3	...	-rk-1	-rk
		R2	-r3	...	-rk-1	-rk
...	...	...	...	...	...	...
k				...	Rk-1	-rk
k+1				...		Rk

При единичной длине ребра симплекса:

;

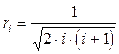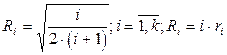
Для 2-х переменных симплекс имеет вид:

X₂

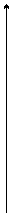+0.58 3

-0.5 0 +0.5

X₁

1 -0.29 2

	x1	x2
	-0.5	-0.29
	0.5	-0.29
		0.58

При отражении наихудшей j-й точки новая вершина получается путём зеркального отображения старой относительно противоположной ей (k-1)-мерной грани исходного симплекса. Координаты новой точки вычисляются по формуле:

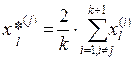
Если в ходе движения симплекса происходит его "вращение" вокруг одной и той же точки (вершины),или возвращение к старой вершине,то в качестве отбрасываемой вершины нужно выбрать ту, в которой целевая функция имеет величину,следующую по порядку за наихудшей вершиной симплекса. Если и это не помогает, то размеры симплекса уменьшают (как правило на 1/4 от исходных).

Если новая (отраженная) вершина симплекса выходит за пределы допустимой области изменения переменных, то так же как и ранее либо заменяют отбрасываемую вершину, либо уменьшают размер симплекса.

Для снижения влияния ошибки наблюдений в каждой точки целесообразно ставить несколько экспериментов, а их результаты-осреднять.

Движение симплекса в процессе поиска оптимального решения имеет вид (при k=2):

Для улучшения сходимости при движении в область оптимума используют различные модификации метода. В частности,деформацию симплекса за счет незеркальности отражения вершины либо с заданным коэффициентом деформации, либо с использованием значений функции отклика в вершинах симплекса в качестве весовых коэффициентов.

Эффективность рассмотренных методов оптимизации зависит от вида поверхности отклика (гребни, овраги, седловые точки и т.д.)

В случае, если функция отклика многоэкстремальна они могут привести в область локального экстремума.Во избежание этого начинать поиск оптимальных решений рекомендуется из нескольких различных начальных точек. Также рассматриваются и другие способы (см. методы нелинейной оптимизации).