Узловая матрица Aн = ïa[i,j]ï, определяется следующим образом: строчками являются узлы схемы, а столбцами соответствующие ветви.
Aн = ïai,jï= 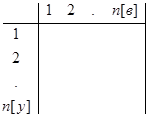 ai,j=
ai,j=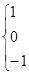
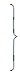 Матрица состоит из 1, 0, -1
Матрица состоит из 1, 0, -1
ai,j=0, если j-ая ветвь не подсоединена к i-ому узлу.
ai,j= +(-) 1, если j-ая ветвь подсоединена к узлу и направлена от узла (к узлу).
 +1
+1
i
-1
Напишем узловую матрицу для своего графа:
 A н=
A н= 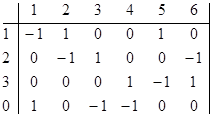 => A н-> Ai -Неопределенная матрица
=> A н-> Ai -Неопределенная матрица
Запишем 1-ый з-н Кирхгофа с помощью матрицы:
A н* i в =0 i в= 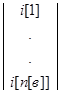 - матрица столбец тока ветвей.
- матрица столбец тока ветвей.
Система алгебраических ур-ний, соответствующая матричному, является системой зависимых ур-ний, т.к. любые ур-ния являются комбинацией других. Для получения линейно независимых ур-ний, один из узлов принимается за базовый, т.е. его потенциал равен нулю, тогда узловая матрица составляется для всех узлов кроме базового
A = 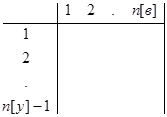 => 1-ый закон Кирхгофа: A н*iв =0
=> 1-ый закон Кирхгофа: A н*iв =0
Определим напряжение в ветвях с потенциалами узлов, введем матрицы напряжений и потенциалов.
U в=

 - Матрица столбец напряжений в ветвях.
- Матрица столбец напряжений в ветвях.
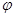 =
=

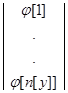 - Матрица столбец потенциалов в узлах.
- Матрица столбец потенциалов в узлах.
Запишем следующее узловое преобразование:
U в = A T* 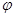
 2014-02-13
2014-02-13 910
910








