Температура. Опять рассмотрим две макроскопические системы, но находящиеся теперь в тепловом контакте, т.е

Опять рассмотрим две макроскопические системы, но находящиеся теперь в тепловом контакте, т.е. системы с заданным числом частиц 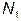и 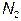, занимающие объемы 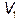и ,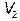

соответственно, но имеющие возможность обмениваться энергией. При этом полная энергия этих систем 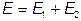сохраняется, так что

,

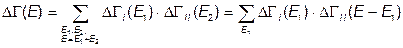где 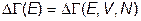и 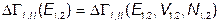- числа микросостояний объединенной системы и ее подсистем I и II.

Для макроскопических систем статистический вес является очень резкой функцией энергии. Поэтому при некотором значении 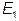одно из слагаемых в последней сумме достигает максимума, причем этот максимум очень резкий. Это слагаемое дает основной вклад в 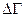, что соответствует наиболее вероятному распределению, т.е. равновесному состоянию. Максимум 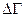определяется равенством

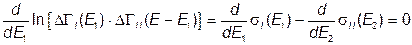
Таким образом, величина

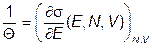(III.3.1)

постоянна по всей системе, находящейся в термодинамическом равновесии, и это соотношение определяет температуру 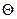в энергетических единицах.

Равенства (III.2.2) и (III.3.1) определяют термодинамические величины – энтропию и температуру – в чисто механических терминах. В этой связи необходимо сделать некоторые уточнения и замечания.

4. Замечания.

1) Утверждение, что для замкнутой системы энергию 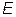можно определить точно, является идеализацией. Действительно, согласно соотношению неопределенностей “энергия-время”, погрешность в определении энергии 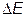связана с полным временем наблюдения :

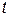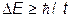, (III.4.1)

т.е. всегда конечна. В классической механике соотношение (III.4.1) формально неприменимо (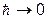), однако в этом случае неопределенность 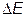связана с флуктуацией энергии вследствие взаимодействия системы с окружающими телами. Поэтому понятие “статистический вес” требует уточнения, так как число микросостояний, совместных с данным макроскопическим, будет зависеть также и от интервала энергий :

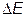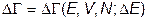(III.4.2)

Поскольку величина 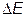произвольна, то определение энтропии (III.2.2) и температуры (III.3.1) теряют, казалось бы, всякий смысл. Однако, для рассматриваемых нами макроскопических тел это не так. Пояснить это проще всего в квазиклассическом приближении. В этом случае одному квантовому состоянию отвечает фазовый объем, равный 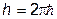. Тогда, например, для идеального одноатомного газа

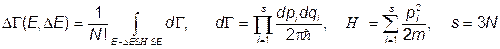(III.4.3)

и, если число степеней свободы 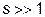, статистический вес практически не зависит от .

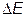Действительно, покажем, что

объем многомерной фигуры сосредоточен вблизи ее поверхности (III.4.4)

Вычислим для этого объем шарового слоя между сферами радиусов 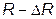и 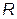при условии .

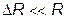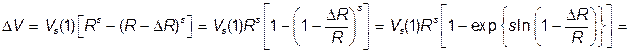
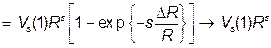, если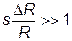

Проиллюстрируем этот вывод на простом примере. Рассмотрим полуметровый арбуз с толщиной корки в 1 см. В трехмерном пространстве

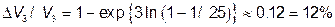
в 25-мерном пространстве имеем

,

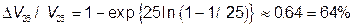в 100 – мерном пространстве

,

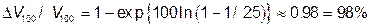поэтому с точки зрения “поглощения” арбузов мы живем в одном из лучших миров.

Для идеального одноатомного газа

, ,

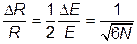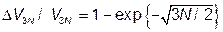т.е. статистический вес с экспоненциальной точностью не зависит от флуктуации 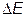. Вычисление (III.4.3) дает

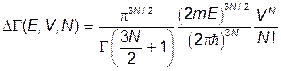(III.4.5)

Множитель 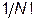учитывает тождественность атомов, т.е. тот факт, что при перестановке

частиц микроскопическое состояние системы не изменяется. Он был введен Гиббсом еще до открытия квантовой механики.

Следует отметить, что утверждение (III.4.4) является “физическим” утверждением, т.е. по словам В.И. Арнольда туманно сформулированным и, вообще говоря, неправильным утверждением. В рассматриваемом случае нарушаться для игольчатых фигур. Однако в физических задачах оно выполняется, и воспоминание об интервале 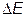остается только в обозначении статистического веса .

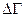2) Для температуры идеального одноатомного газа 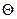, согласно (III.3.1) и (III.4.5), имеем

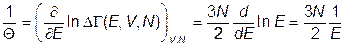
Учитывая, что для одноатомного газа 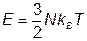, получаем 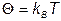, что согласуется с (I.1.3). Выражая энергию через температуру и логарифмируя (III.4.5), при 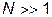получаем

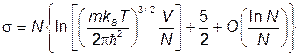(III.4.6)

Поэтому в термодинамическом пределе (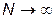, , 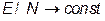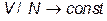) энтропия является аддитивной величиной, что было бы не так, если не учитывать фактор 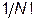(парадокс Гиббса). Комбинация, возникающая в (III.4.6)

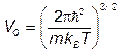(III.4.7)

имеет размерность объема и называется “квантовым объемом”.

3) Вспоминая Людвига Эдуарда Больцмана (1844-1906), один из крупнейших физиков ХХ века Арнольд Иоганнес Вильгельм Зоммерфельд (1968-1951) пишет: “На памятнике Больцману на центральном кладбище в Вене, как квинтэссенция его работ сделана надпись

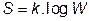
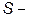это общепринятое обозначение термодинамической энтропии, определяемой вторым началом; 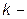так называемая постоянная Больцмана, связанная с универсальной газовой постоянной; 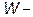вероятность рассматриваемого состояния[1], число, которое Больцман научил определять чисто арифметически, посредством подсчета всех возможных состояний. Благодаря созданию этих понятий Больцман является ученым, проложившим путь

квантовой теории, что всегда с радостью признавал Макс Планк ” и в другом месте (в воспоминаниях об Альберте Эйнштейне) – “идею Больцмана о том, чтобы основывать термодинамику на статистике, энтропию – на расчете вероятностей Эйнштейн осуществил во многих применениях как “ принцип Больцмана”.

В то же время в прекрасной книге Риого Кубо “Статистическая механика” можно прочесть: На центральном кладбище прекрасной Вены путешественники могут увидеть памятник Людвигу Больцману (1844-1906 гг.), на котором навсегда запечатлен его ценнейший дар человечеству, а именно формула

.

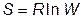Несущественное противоречие между утверждениями Планка и Кубо (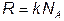- газовая постоянная) разрешилось следующим образом. Один из студентов факультета “Т”, слушавших эти лекции, как участник хора МИФИ очутился в Вене на юбилее МАГАТЭ. Отыскав могилу Больцмана, он подтвердил правоту Зоммерфельда, специально подчеркивая наличие точки в формуле для энтропии. По-видимому, сам Больцман никогда не писал эту формулу в явном виде. Ее дал Планк в своих лекциях по теории теплового излучения, подчеркнув, что она определяет энтропию однозначно, не оставляя неопределенности в выборе аддитивной постоянной. Поэтому безразмерная энтропия 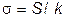в формуле (III.2.2) по праву называется планковской энтропией.