Интегральные уравнения для краевых задач

Полученные нами в предыдущей лекции свойства потенциалов позволяют решать задачи Дирихле и Неймана для любых областей, ограниченных достаточно гладкими поверхностями, приведением их к интегральным уравнениям.

Рассмотрим решение внутренней задачи Дирихле. Будем предполагать, что искомая функция 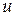есть потенциал двойного слоя 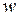с неизвестной пока плотностью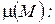

.

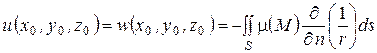Как известно, потенциал двойного слоя есть гармоническая функция. Мы должны подчинить 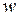тому условию, чтобы ее предельное значение изнутри равнялось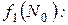

.

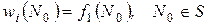Из теоремы 2 лекции 23 имеем

.

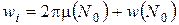Таким образом, для неизвестной плотности 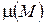получим уравнение

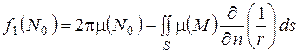
Здесь 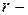расстояние между точкам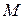и и 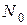поверхности .

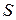Полагая, 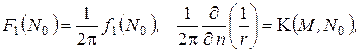приходим к уравнению

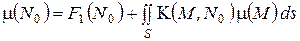. (3)

Интегральное уравнение (3) называется интегральным уравнением Фредгольма второго рода. К изучению таких уравнений мы вскоре перейдем.

Так же точно можно свести и задачу Дирихле для внешней области, ограниченной поверхностью 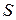, т.е. для бесконечной области, границей которой служит 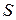, опять к уравнению Фредгольма второго рода.

В самом деле, отыскивая решение снова в виде потенциала двойного слоя из условия 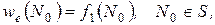получим (см. теорему 2 лекции №23), аналогично прежнему, для неизвестной плотности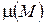

.

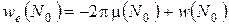Откуда

;

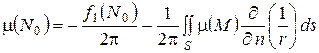вводя обозначение 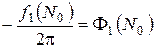, получим

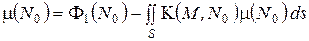. (4)

Это уравнение есть уравнение того же типа и рода, что и предыдущее.

К интегральным уравнениям приводятся также внутренняя и внешняя задачи Неймана.

Будем искать решение внутренней задачи Неймана в виде потенциала простого слоя.

.

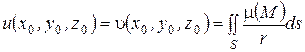как и выше из формулы (5) лекции №23 имеем

,

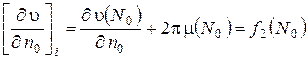откуда

.

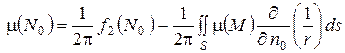Полагая 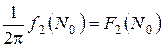, получим для 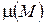уравнение

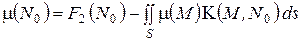. (5)

Наконец, если искать решение внешней задачи Неймана в виде потенциала простого слоя 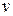будем иметь согласно формулы (5) лекции №23 соотношение

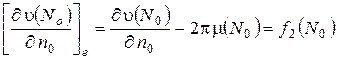
или

.

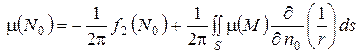Полагая

,

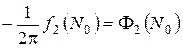получим для неизвестной плотности 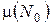уравнение

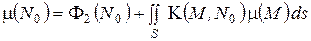. (6)

Если нам удастся найти такие функции 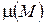, удовлетворяющие уравнениям (3) - (6), то соответствующие задачи математической физики будут решены.