Для возможного строгого установления свойств потенциалов простого и двойного слоя необходимо подчинить ряду требований те поверхности, на которых расположены эти слои.
Будем называть замкнутую поверхность 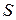 поверхностью Ляпунова, если выполнены следующие три условия:
поверхностью Ляпунова, если выполнены следующие три условия:
1. Поверхность 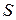 имеет везде касательную плоскость.
имеет везде касательную плоскость.
2. Вокруг каждой точки 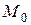 поверхности можно описать такой шар радиуса
поверхности можно описать такой шар радиуса 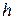 , не зависящего от
, не зависящего от 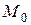 , внутрь которого попадет лишь участок
, внутрь которого попадет лишь участок 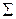 поверхности
поверхности 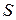 , встречающий прямые, параллельные нормали
, встречающий прямые, параллельные нормали 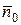 в точке
в точке 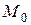 , не более чем один раз.
, не более чем один раз.
3. Если 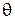 - острый угол, образованный нормалями к
- острый угол, образованный нормалями к 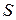 в двух ее точках
в двух ее точках 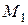 и
и 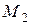 , и
, и 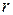 - расстояние между этими двумя точками, то имеет место неравенство
- расстояние между этими двумя точками, то имеет место неравенство
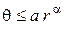 ,
,
где 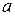 и
и 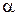 - постоянные числа, причем
- постоянные числа, причем 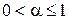 .
.
Условие 1) дает возможность в каждой точке 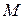 поверхности Ляпунова построить местную прямоугольную систему координат
поверхности Ляпунова построить местную прямоугольную систему координат 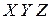 , Беря точку
, Беря точку 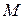 за начало координат, касательную плоскость в точке
за начало координат, касательную плоскость в точке 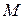 за плоскость
за плоскость 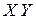 и нормаль поверхности в точке
и нормаль поверхности в точке 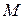 за ось
за ось 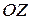 . Условие 2) показывает, что в этой местной системе координат уравнение части поверхности
. Условие 2) показывает, что в этой местной системе координат уравнение части поверхности 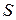 , заключенной внутри сферы
, заключенной внутри сферы  с центром в точке
с центром в точке 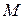 и радиусом
и радиусом 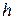 , может быть представлено в виде, разрешенном относительно
, может быть представлено в виде, разрешенном относительно 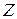 :
:
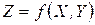 .
.
Из условия 3) следует, что частные производные 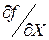 и
и 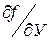 являются непрерывными функциями
являются непрерывными функциями 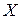 и
и 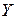 .
.
 2014-02-13
2014-02-13 1193
1193
