Пусть 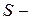 замкнутая достаточно гладкая поверхность. Обозначим через
замкнутая достаточно гладкая поверхность. Обозначим через 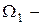 область, ограниченную этой поверхностью, а через
область, ограниченную этой поверхностью, а через 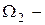 бесконечную область, внешнюю по отношению к
бесконечную область, внешнюю по отношению к 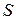 , также ограниченную поверхностью
, также ограниченную поверхностью 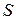 .
.
Рассмотрим четыре задачи:
1. Внутренняя задача Дирихле. Найти функцию 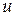 , гармоническую в
, гармоническую в 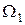 , при условии
, при условии
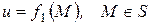 .
.
2. Внешняя задача Дирихле. Найти функцию 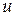 , гармоническую в
, гармоническую в 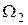 при условиях:
при условиях:
а) 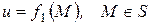 ,
,
б) 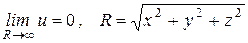 .
.
3. Внутренняя задача Неймана. Найти функцию 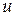 , гармоническую в
, гармоническую в 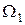 , при условии
, при условии
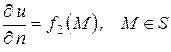 .
.
4. Внешняя задача Неймана. Найти функцию, гармоническую в 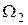 , при условиях:
, при условиях:
а) 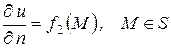
б) 
Прежде чем намечать пути решения этих задач, займемся их исследованием.
Теорема 1. Решение задачи Дирихле, внутренней или внешней, единственно.
Доказательство. Рассмотрим сначало внутреннюю задачу Дирихле. Предположим, что существуют два решения 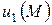 и
и 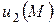 одной и той же задачи Дирихле. Тогда из разность
одной и той же задачи Дирихле. Тогда из разность
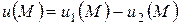
будет гармонической функцией, равной нулю на 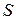 . Отсюда из принципа максимума следует. что
. Отсюда из принципа максимума следует. что 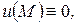 т.е.
т.е. 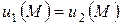 во всей области
во всей области 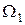 , так как в противном случае она должна была бы достигать внутри области
, так как в противном случае она должна была бы достигать внутри области 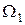 положительного наибольшего значения или отрицательного наименьшего значения, что невозможно.
положительного наибольшего значения или отрицательного наименьшего значения, что невозможно.
Рассмотрим теперь внешнюю задачу Дирихле. Как и выше, предположим, что существуют два решения 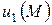 и
и 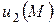 . Тогда из разность
. Тогда из разность 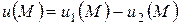 будет гармонической функцией, равной нулю на
будет гармонической функцией, равной нулю на 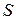 и
и 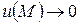 при
при 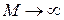 , т.е. для любого
, т.е. для любого 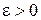 можно указать такое
можно указать такое 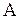 , что
, что 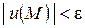 при
при 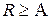 . Пусть
. Пусть 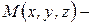 произвольная точка бесконечной области
произвольная точка бесконечной области 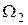 . Проведем сферу
. Проведем сферу 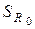 с центром в начале координат и радиусом
с центром в начале координат и радиусом 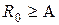 столь большим, чтобы точка
столь большим, чтобы точка 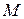 и поверхность
и поверхность 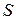 лежали внутри этой сферы. Тогда
лежали внутри этой сферы. Тогда 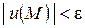 , что следует из теоремы о максимуме и минимуме, примененной к конечной области, заключенной между
, что следует из теоремы о максимуме и минимуме, примененной к конечной области, заключенной между 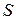 и
и 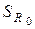 . В силу произвольности
. В силу произвольности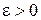 заключаем, что
заключаем, что 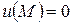 , а так как
, а так как 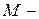 любая точка области
любая точка области 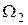 , то
, то 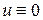 в
в 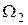 , т.е.
, т.е.  .
.
Теорема 2. Решение внешней задачи Неймана, имеющее непрерывные вплоть до границы производные первого порядка, единственно, решение внутренней задачи Неймана определено с точностью до произвольной постоянной.
Доказательство. Рассмотрим сначала внутреннюю задачуНеймана. Пусть 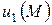 и
и 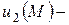 два решения задачи Неймана в области
два решения задачи Неймана в области 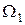 с границей
с границей 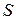 . Удовлетворяющие одному и тому же граничному условию
. Удовлетворяющие одному и тому же граничному условию
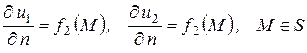 .
.
Тогда из разность 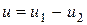 будет гармонической функцией внутри области
будет гармонической функцией внутри области 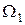 , для которой
, для которой 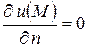 при
при 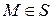 .
.
Воспользуемся первой формулой Грина для гармонических функций
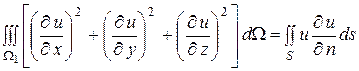 .
.
Правая часть равна нулю, значит, и левая часть равна нулю. Тогда в силу непрерывности функции 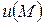 и ее первых производных следует, что
и ее первых производных следует, что
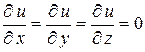 .
.
т.е. 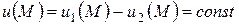 , что и требовалось доказать.
, что и требовалось доказать.
Отметим, что внутренняя задача Неймана не всегда разрешима. Для ее разрешимости необходимо, чтобы
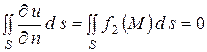 .
.
Необходимость вытекает из свойства гармонических функций (см. Лекцию №19). Для рассмотрения внешней задачи возьмем сферу 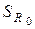 радиуса
радиуса 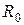 , где
, где 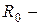 достаточно большое число, и пусть
достаточно большое число, и пусть 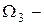 объем, заключенный между
объем, заключенный между 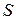 и
и 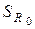 . Далее пусть
. Далее пусть 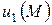 и
и 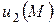 - два решения внешней задачи Неймана, удовлетворяющие одному и тому же граничному условию. Тогда их разность есть гармоническая функция в бесконечной области для которой
- два решения внешней задачи Неймана, удовлетворяющие одному и тому же граничному условию. Тогда их разность есть гармоническая функция в бесконечной области для которой
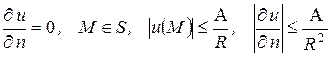 . (1)
. (1)
Теперь, применяя формулу Грина для гармонических функций к области  , получим
, получим
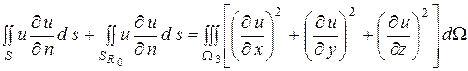
или в силу (1),
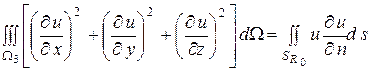 . (2)
. (2)
В силу оценок (1) имеем
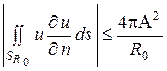 .
.
Тогда из (2) получаем, что при достаточно большом 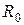 имеем
имеем
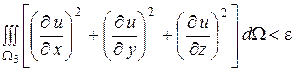
при любом 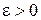 , что возможно лишь при условии
, что возможно лишь при условии
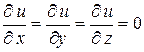 .
.
Значить, 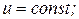 так как
так как 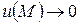 при
при 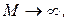 то
то 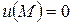 , т.е.
, т.е. 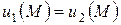 .
.
 2014-02-13
2014-02-13 1147
1147
