Коэффициенты затухания ультразвука воды и некоторых биологических тканей
(n – частота, при которой проводили измерения)
Вода 1,00 0,01
Плазма крови 0,87 2,0
Кровь 1,00 2,5
Жировая ткань 0,87 4,5
Мозг 0,87 14
Мышцы 0,87 16
Печень 0,87 15
Кожа 1,00 40
Кость 0,88 71
Примечание. Приведенные в таблице данные получены разными исследователями при измерениях на тканях человека.
Ультразвук, обладающий малой длиной волны, сильно поглощается в воздухе, но в жидкостях его поглощение меньше, так как плотность жидкостей в тысячи раз больше плотности газов. В жидкостях с большой вязкостью поглощение ультразвука возрастает. Сильно уменьшается интенсивность ультразвука при распространении его в биологических тканях, выполняющих в организме поддерживающую и опорную функции, из-за многочисленных отражений на волокнистых соединительных структурах (см. табл.).
Пусть звук создается точечным источником, мощность которого (количество испускаемой им в единицу времени энергии по всем направлениям) равна N. Окружим мысленно источник звука сферой радиуса R. Если пренебречь поглощением, то через поверхность сферы будет проходить такое же количество энергии в единицу времени, какое испускается всей поверхностью источника, т. е. AnR2I = N, где I – количество энергии, проходящей через единицу площади поверхности сферы в единицу времени, иными словами, интенсивность звука на ее поверхности. Отсюда получаем
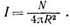
Следовательно, интенсивность сферической звуковой волны убывает обратно пропорционально квадрату расстояния от источника звука.
 Итак, затухание звука обусловлено тремя причинами: поглощением, рассеянием на неоднородностях среды и увеличением поверхности волнового фронта с расстоянием. Последний фактор можно уменьшить, если создать условия для распространения звуковой волны с плоским фронтом. Тогда в однородной среде ослабление звука происходит только за счет его поглощения. Такие условия создаются, например, в трубах. Переговорными трубами издавна пользовались на кораблях для переговоров между его отсеками. На малом ослаблении звука в трубах основано действие фонендоскопа.
Итак, затухание звука обусловлено тремя причинами: поглощением, рассеянием на неоднородностях среды и увеличением поверхности волнового фронта с расстоянием. Последний фактор можно уменьшить, если создать условия для распространения звуковой волны с плоским фронтом. Тогда в однородной среде ослабление звука происходит только за счет его поглощения. Такие условия создаются, например, в трубах. Переговорными трубами издавна пользовались на кораблях для переговоров между его отсеками. На малом ослаблении звука в трубах основано действие фонендоскопа.
Звуки какой-либо одной частоты, так называемые «чистые тоны», редко встречаются в природе. Гораздо чаще приходится иметь дело со звуковыми колебаниями, график которых изображается не синусоидой, а сложной периодической функцией. Согласно теореме Фурье любую сложную периодическую функцию x(t) можно представить в виде суммы гармонических составляющих
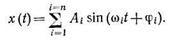
Первый член в этой формуле характеризует основной тон, а остальные члены с более высокими частотами представляют собой дополнительные тоны (обертоны), определяющие тембр звука. Например, прямоугольные колебания с любой точностью можно представить в виде суммы синусоидальных колебаний. На рисунке пунктиром изображен график прямоугольных колебаний, а кривые А, Б и В – графики трех синусоидальных колебаний; кривая Г получена сложением трех синусоид и довольно близко подходит к пунктирной кривой. Если количество составляющих синусоид увеличить, то результирующая кривая Г все больше будет приближаться к прямоугольной.
 Основной тон вместе с обертонами определяет акустический спектр звука. Для графического изображения сложного звука удобно строить спектральные диаграммы, на которых по горизонтальной оси откладывают частоты колебаний, а по вертикальной оси – величины амплитуд или интенсивностей основного тона и обертонов в соответствующем масштабе. На рисунке 13,6 изображен линейчатый спектр, состоящий из основного тона и двух гармоник, соответствующих колебаниям А, Б и В на рисунке 13, а. В отличие от музыкальных звуков, характеризуемых линейчатыми спектрами и состоящих из конечного числа обертонов, шумы представляют собой негармонические звуки, частота и амплитуда которых изменяются со временем, в результате чего в спектре шума присутствует огромное число обертонов, и такие спектры имеют вид, изображенный на рисунке 14. От вида спектра зависит и восприятие шума (треск, шипение, щелканье).
Основной тон вместе с обертонами определяет акустический спектр звука. Для графического изображения сложного звука удобно строить спектральные диаграммы, на которых по горизонтальной оси откладывают частоты колебаний, а по вертикальной оси – величины амплитуд или интенсивностей основного тона и обертонов в соответствующем масштабе. На рисунке 13,6 изображен линейчатый спектр, состоящий из основного тона и двух гармоник, соответствующих колебаниям А, Б и В на рисунке 13, а. В отличие от музыкальных звуков, характеризуемых линейчатыми спектрами и состоящих из конечного числа обертонов, шумы представляют собой негармонические звуки, частота и амплитуда которых изменяются со временем, в результате чего в спектре шума присутствует огромное число обертонов, и такие спектры имеют вид, изображенный на рисунке 14. От вида спектра зависит и восприятие шума (треск, шипение, щелканье).
 2014-02-13
2014-02-13 1362
1362








