Сумма реальных расходов со штрафом составит

S(X) = F(X) + R(X) = (75 + l₁ + 2l₃ )X₁ + 800/X₁ +

+ (78 + 2.5l₃)X₂ + 1600/X₂ - 5l₁ +16l₃.

Найдем минимум S(X), дифференцируя эту функцию по X₁ и X₂:

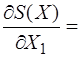75 + l₁ + 2l₃ - 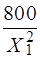= 0,

откуда

X₁ = 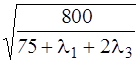; (3.8)

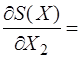78 + 2.5l₃ - 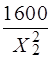= 0.

Тогда

X₂ = 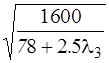. (3.9)

Анализ (3.8) и (3.9) показывает, что с увеличением штрафов l₁ и l₃ значения X₁ и X₂ , дающие min условной суммы расходов, сокращаются: высокий штраф за использование ресурса снижает его потребление. С уменьшением X₁ и X₂ сокращаются и нарушения тех ограничений, которые были отмечены в исходном варианте. Таким образом, точка (X₁ и X₂) при увеличении малыми шагами штрафов l₁ и l₃ приближается к границе области допустимых значений переменных (заштрихованная область на рис. 3.5).

При некоторых значениях l₁^k, l₂^k, соответствующих точке (X₁^k, X₂^k), для которой все частные производные равны нулю, окажется на границе допустимой области. Доказано, что именно эти значения являются оптимальными: обеспечивают min целевой функции. В отличие от задач ЛП оптимальная точка нелинейной задачи лежит в общем случае не в вершине, а на одной из сторон (граней) области допустимых решений.

Итак, задача состоит в подборе таких значений l_i (по числу ограничений), чтобы в одной из пограничных точек допустимой области частные производные 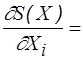0 для "X_i. Значения l_i находятся методом итераций. В качестве исходного приближения можно выбрать точку, дающую min реальных расходов. Задаемся исходными значениями штрафов l_i за привлечение единицы излишних ресурсов. В исходной точке первое из неравенств не нарушено, поэтому логично предположить l ₁ = 0. Третье неравенство нарушено, и для баланса необходимо положить l ₃ > 0. Численный выбор l ₃ не принципиален, а влияет только лишь на число итераций. Далее действуем по алгоритму:

1. Находим для очередной точки X = (X₁, X₂) частные производные функции S(X) по X₁ и X₂ . Пусть их значения равны

P₁ = 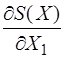и P₂ = .

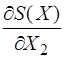2.

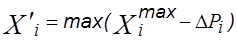Находим новые значения переменных X = (X₁, X₂) по формуле

3. Находим для новой точки X = (X₁, X₂) величину нарушений неравенств. Например, нарушение первого неравенства составляет

f₁ = x ₁ - 5, третьего f₃ = 2 x ₁ + 2.5 x ₂ - 16.

4. Находим новые значения штрафов l_i исходя из прежних значений l_i: l_i = max (0; l_i + Df_i), где f_i - величина нарушений, принимаемая из п. 3; D - шаг из п. 2.

После этого начинают новый цикл расчетов, переходя к п.1. При этом вычисленные в предыдущем цикле значения переменных и штрафов принимают в новом цикле за исходные. Оптимум будет найден, если в очередном цикле все 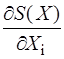, вычисленные в п.1, равны нулю, т.е. найденная точка лежит на границе допустимой области.

Пример. x ₁ = 3,26; x ₂ = 4,53; l₁ = 0; l₃ = 8; D = 0,05

1. P₁ = 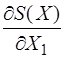= 75 + l₁ + 2l₃ - 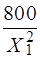= 75 + 0 + 2×8 - 800/3,26 ² = 15,7;

P₂ = 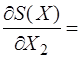78 + 2,5l₃ - 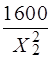= 78 + 2,5×8 - 1500/4,53² =20,0.

2. Находим нарушения неравенств при новых значениях переменных:

x ₁ = max (x ₁^min; x ₁ - DP₁) = max (2; 3,25 – 0,05×15,7) = 2,48;

x ₂ = max (x ₂^min; x ₂ - DP₂) = max (4; 4,53 – 0,05×20,0) = 4,0.

3. f₁ = x ₁ - 5 = - 2,52; f₃ = 2 x ₁ + 2,5 x ₂ - 16 = 2×2,48 + 2,5×4 - 16 = - 1,04.

4. Корректируем штрафы:

l₁ = max (0; l₁ + Df₁) = max (0; 0 + 0,05×(-2,52)) = 0;

l₃ = max (0; l₃ + Df₃) = max (0; 8 + 0,05×(-1,04)) = 7,95.

Первый цикл закончен. Переходим ко второму циклу.

1. P₁ = 75 + l₁ + 2l₃ - 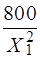= 75 + 0 + 2×7,95 - 800/2,48² = - 39,2.

Прежде чем продолжить счет, проанализируем P₁ в первом и втором циклах. Можно увидеть, что 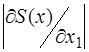возросла с 15,7 до 39,2 и так как в п. 2. поправка к значению X₁ пропорциональна P₁, значит, во втором цикле поправка будет больше, чем в первом.

Следовательно, процесс не сходится к определенным значениям X₁. Это говорит о большой величине шага D. Уменьшим его до D= 0,02,

тогда 1. P₂ = 78 + 2,5l₃ - 1600/X₂² =78 + 2,5×7,25 - 1600/4² = - 2,1.

2. x ₁ =max (2; 2,48 – 0,02×(- 39,2) = 3,26;

x ₂ = max (4; 4 – 0,02×(- 2,1) = 4,04.

3. f₁ =3,26 - 5 = -1,74;

f₃ = 2×3,26 + 2,5×4,04 - 16 = 0,62.

4. l₁ = max (0; 0 + 0,02×(-1,74)) = 0;

l₃ = max (0; 7,95 + 0,02×0,62) = 7,96.

Второй цикл окончен. Сведем дальнейшие расчеты в табл. 3.1.

Табл. 3.1

№ циклов	P1	P2	X1	X2	f1	f3	l1	l3
	15,6		2,95	4,04	- 2,05			7,96
	-1,0	- 0,1	2,97	4,04	- 2,03	0,04		7,96
	0,2	- 0,1	2,96	4,04	- 2,04	0,02		7,96

X₁ = 2,96;

X₂ = 4,04.

Как видно из табл. 3.1, после четвертого цикла решение стабилизируется в точке (X₁ = 2,96; X₂ = 4,04). При этом производные P₁ и P₂ оказываются близкими к нулю, третье неравенство выполняется как равенство (невязкой f₃ = 0,02 можно пренебречь). Таким образом, точка, найденная на границе допустимой области, представляет собой оптимальное решение задачи. Сходимость оказалась весьма быстрой ввиду удачного выбора первоначального значения l₃. При менее удачной оценке l₃ число шагов оказалось бы больше.