A. Характер распределения ошибок в реальных каналах

ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ ОШИБОК В РЕАЛЬНЫХ КАНАЛАХ СВЯЗИ

Одним из основных параметров последовательности ошибок является частота появления ошибок p_L. Частость появления ошибок (или просто частость ошибок) определяется как отношение числа ошибок М_ош =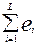, появившихся за определенный отрезок времени t, к общему числу переданных символов L:

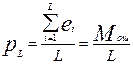
При достаточно большом L частость ошибок сходится с вероятностью появления ошибки (вероятность ошибки) p. Значения p для различных типов каналов приведены в таблице 3.1.

В течение длительного времени, когда отсутствовали статистические данные реальных каналов связи, предполагалось, что ошибки в каналах связи появляются независимо. При таком распределении ошибок значение i-го элемента последовательности ошибок Е не зависит от того, какое значение принимает любой другой j-й элемент данной последовательности.

Пусть Р{e_i=1}=p, P{(e_i=1)/(e_j=1)} — вероятность приема i-го элемента с ошибкой (e_i=1) при условии, что ошибка произошла на j-м месте (e_j=1), а Р{(e_i=1)/(e_j=0)} — вероятность приема i-го элемента с ошибкой при условии, что j-й элемент принят правильно. Ошибки появляются независимо, если выполняется условие:

Р{(e_i=1)/(e_j=1)}=Р{(e_i=1)/(e_j=0)}=Р{e_i=1}=p

В противном случае появление ошибок является зависимым событием.

При независимых ошибках достаточно знать значение единственного параметра р, чтобы определить распределение любой случайной величины. Для этого достаточно воспользоваться схемой Бернулли. В частности, вероятность появления в n-элементной комбинации ровно i ошибок P(i,n) определяется биномиальным распределением:

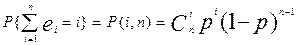(0 ≤ i ≤ n).

Вероятность приема комбинации без ошибки P(0,n)=(1 — p)ⁿ = qⁿ . Следовательно, вероятность появления искаженной комбинации, т.е. комбинации, содержащей хотя бы одну ошибку,

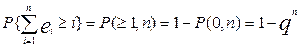, при np «1, P(≥1,n) ≈ np.

Вероятность появления m и более ошибок в комбинации длины n:

.

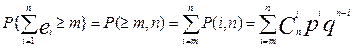Иногда (при m<n/2) для вычисления P(≥m,n) удобнее пользоваться формулой, полученной из условия, что

:

.

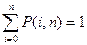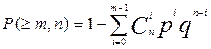Многочисленные исследования реальных каналов связи не подтвердили гипотезу о независимом характере появления ошибок.

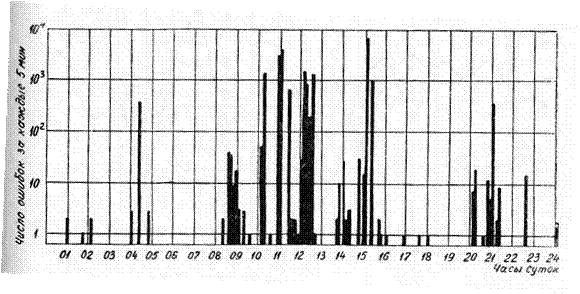Рис.3.1

Данные исследования показали, что ошибки появляются группами (пачками). Частость ошибок во время появления группы ошибок возрастает и становится значительно больше вероятности р. На рисунке 3.1 в качестве примера, иллюстрирующего групповой характер появления ошибок, приведено абсолютное число ошибок, появляющихся за каждые пять минут суток в кабельном телефонном канале связи. Это число определялось по результатам испытания канала в течение шести суток. Ошибки, как показано на рисунке 3.1 группируются в определенные промежутки времени. В ночное время число ошибок в подавляющем большинстве пятиминутных сеансов равно нулю или меньше десяти. В первой половине дня число ошибок за пятиминутные интервалы редко бывает равно нулю, а в большинстве превышает сотни и тысячи ошибок. Испытания проводились на скорости телеграфирования N=1200 бод, поэтому L=5·60·1200=3.6·10⁵ элементов. Частость ошибок p_L в ночное время колеблется в пределах 0÷3·10^-5, а в дневное время — 0÷10^-2.

Таким образом, появление ошибок в реальных каналах является зависимым событием, поэтому схема Бернулли не применима. Расчеты по формулам, полученным на основе данной схемы, приводят к значительным, а во многих важных для практики случаях и недопустимым погрешностям. Групповой характер появления ошибок проявляется во всех статистических характеристиках последовательности ошибок. Поэтому для математического описания этой последовательности недостаточно знать один параметр р, а необходимо определить дополнительные параметры, учитывающие степень зависимости появления ошибок в реальных каналах.