Для того, чтобы стационарная механическая система с идеальными конечными связями находилась в положении равновесия, необходимо и достаточно, чтобы в этом положении сумма элементарных работ внешних сил на любых возможных перемещениях системы равнялась нулю.
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Положением равновесия называется такое положение системы, в котором система будет находиться все время, если в начальный момент времени она находилась в этом положении, и скорости всех ее точек были равны нулю.
Положение системы будет положением равновесия в том случае, когда в этом положении системы
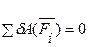 .
.
Это равенство выражает принцип возможных перемещений:
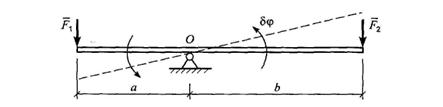
Принцип возможных перемещений был известен со времен Архимеда под названием «золотого правила механики» и применялся к простейшим механизмам. Рассмотрим в качестве примера рычаг Архимеда Рычаг имеет одну степень свободы - может вращаться вокруг точки О. Равновесие имеет место, когда элементарная работа при повороте рычага на элементарный угол δφ равна нулю.
Общее уравнение динамики относится к уникальному методу исследования задач динамики механических систем.
Рассмотрим голономную систему N материальных точек, подчиненную идеальным связям. Каждая точка системы движется согласно основному закону динамики
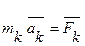
где тk - масса k -ой точки системы, 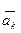 - ее ускорение,
- ее ускорение, 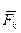 - равнодействующая внешних сил, приложенных к k -ой точке (k = 1,2,..., N).
- равнодействующая внешних сил, приложенных к k -ой точке (k = 1,2,..., N).
Если ввести силу инерции 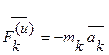 , то основной закон динамики можно записать в форме равновесия сил
, то основной закон динамики можно записать в форме равновесия сил
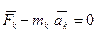 ,
,
или
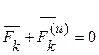 . (k = l,2,...,N)
. (k = l,2,...,N)
Полученное выражение соответствует принципу Д'Аламбера: совокупность всех внешних сил, действующих на механическую систему и сил инерции образует в каждый момент времени уравновешенную систему сил.
Мысленно зафиксируем время t и сообщим каждой точке системы одно из возможных перемещений 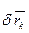 . Умножим скалярно каждое слагаемое на
. Умножим скалярно каждое слагаемое на 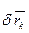 , затем сложим все N полученных уравнений между собой, получим
, затем сложим все N полученных уравнений между собой, получим
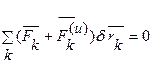 ,
,
т.е. 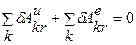 , (k = l,2,...,N), (*)
, (k = l,2,...,N), (*)
здесь: 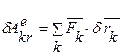 . - элементарная работа внешних сил, на одном из возможных перемещений
. - элементарная работа внешних сил, на одном из возможных перемещений 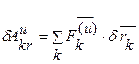 - элементарная работа сил инерции на том же возможном перемещении.
- элементарная работа сил инерции на том же возможном перемещении.
Уравнение (*) называется общим уравнением динамики:
 2014-02-13
2014-02-13 405
405








