К собственным полупроводникам относят химически чистые полупроводники. Классическими примерами собственных полупроводников являются германий (Ge) и кремний (Si) высокой чистоты.
В собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный.
При 0 К и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики.
При повышении же температуры электроны с верхних уровней валентной зоны могут быть переброшены на нижние уровни зоны проводимости (рис. 3.7).
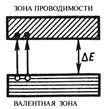
Рис. 3.7
При наложении на кристалл электрического поля электроны в зоне проводимости перемещаются против поля и создают электрический ток. Составляющая проводимости собственных полупроводников, обусловленная электронами, называется электронной проводимостью или проводимостью n-типа (от лат. negative – отрицательный).
В результате тепловых забросов электронов из валентной зоны в зону проводимости в валентной зоне возникают вакантные состояния, получившие название дырок. Во внешнем электрическом поле на освободившийся уровень валентной зоны (дырку) в одном месте кристалла может переместиться электрон с соседнего уровня и дырка появится в другом месте, откуда «ушёл» электрон и т.д. Такой процесс заполнения дырок электронами равносилен перемещению дырок в направлении, противоположном движению электронов, как если бы дырка была некоторой частицей и обладала положительным зарядом, равным по величине заряду электрона. Дырка представляет собой условную частицу, или, как говорят, квазичастицу. Составляющую проводимости собственных полупроводников, обусловленную квазичастицами – дырками называют дырочной проводимостью или проводимостью р-типа (от лат. positive – положительный).
Число электронов в зоне проводимости равно числу дырок в валентной зоне. Следовательно, в собственных полупроводниках концентрация электронов в зоне проводимости равна концентрации дырок в валентной зоне 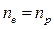 .
.
Определенная концентрация электронов и дырок в полупроводнике при Т = const устанавливается в результате действия двух процессов – термической генерации свободных носителей тока и их рекомбинации. В полупроводнике происходит не только переброс электронов из валентной зоны в зону проводимости, но и переход электронов из зоны проводимости в валентную (дырочную) зону. При обратном переходе электрон и дырка связываются, и пара носителей уничтожается. Этот акт называют рекомбинацией носителей.
В собственном полупроводнике уровень Ферми при Т = 0 К находится в середине запрещённой зоны (рис. 3.8).
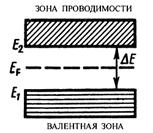
Рис. 3.8
Действительно, при появлении электрона в зоне проводимости в валентной зоне обязательно возникает дырка. Следовательно, энергия активации 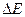 , затраченная на образование пары носителей тока, должна делиться на две равные части, откуда
, затраченная на образование пары носителей тока, должна делиться на две равные части, откуда
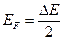 .
.
Плотность тока 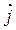 при собственной проводимости полупроводника складывается из плотности тока электронов и дырок:
при собственной проводимости полупроводника складывается из плотности тока электронов и дырок:
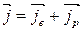 . (3.1)
. (3.1)
Обозначим равные друг другу концентрации электронов и дырок 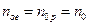 и средние скорости упорядоченного движения электронов и дырок
и средние скорости упорядоченного движения электронов и дырок 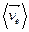 и
и 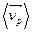 . Тогда
. Тогда
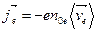 ,
, 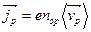 . (3.2)
. (3.2)
Используя формулу закона Ома в дифференциальной форме
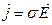 , (3.3)
, (3.3)
и формулы (3.2), получим:
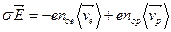 , (3.4)
, (3.4)
затем, если разделить обе части (3.4) на 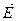 и ввести подвижность электронов и дырок
и ввести подвижность электронов и дырок 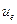 и
и 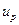
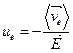 и
и 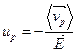 , (3.5)
, (3.5)
то найдем
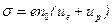 . (3.6)
. (3.6)
Так как для собственных полупроводников 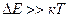 , то распределение Ферми-Дирака (2.9) переходит в распределение Максвелла-Больцмана (2.3). Положив в (2.9)
, то распределение Ферми-Дирака (2.9) переходит в распределение Максвелла-Больцмана (2.3). Положив в (2.9) 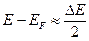 ,
,
получим
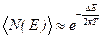 . (3.7)
. (3.7)
Концентрация 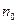 электронов и дырок, очевидно, пропорциональна
электронов и дырок, очевидно, пропорциональна 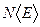 , т.е.
, т.е.
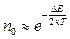 . (3.8)
. (3.8)
Подставляя (3.8) в (3.6), получим, что удельная проводимость собственных полупроводников быстро растёт с температурой, изменяясь по закону
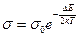 , (3.9)
, (3.9)
где 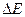 – ширина запрещенной зоны,
– ширина запрещенной зоны, 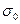 – величина, изменяющаяся с температурой гораздо медленнее, чем экспонента, в связи с чем ее можно в первом приближении считать постоянной.
– величина, изменяющаяся с температурой гораздо медленнее, чем экспонента, в связи с чем ее можно в первом приближении считать постоянной.
Логарифмируя (3.9), получим
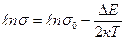 .
.
Видно, что зависимость 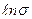 от
от 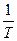 линейная. Примерный график этой зависимости приведён на рис. 3.9.
линейная. Примерный график этой зависимости приведён на рис. 3.9.
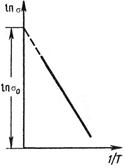
Рис. 3.9
По наклону отрезка прямой можно определить ширину запрещенной зоны 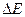 , а по пересечению продолжения прямой с осью
, а по пересечению продолжения прямой с осью 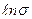 – величину
– величину 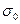 (прямая отсекает на оси ординат отрезок, равный
(прямая отсекает на оси ординат отрезок, равный 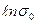 ).
).
 2015-01-21
2015-01-21 738
738








