Распределение Максвелла

При столкновении молекулы газа изменяют свои скорости. Изменение скорости молекул происходит случайным образом. Нельзя заранее предсказать, какой численно скоростью будет обладать данная молекула: эта скорость случайна.

Распределение молекул по модулям скоростей описывают с помощью функции распределения f(v):

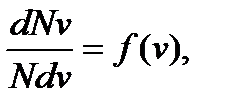(13)

где отношение 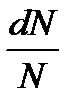— равно доле молекул, скорости которых лежат в интервале от v до v + dv. dv – ширина интервала (рис. 2).

Рис. 2. Интервал скоростей

Зная вид f(v), можно найти число молекул Δ N_V из числа данных молекул N, скорости которых попадают внутрь интервала скоростей от v до v + Δv. Отношение

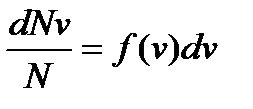(14)

дает вероятность того, что скорость молекулы будет иметь значение в пределах данного интервала скоростей dv.

Функция f(v) должна удовлетворять условию нормировки, то есть должно выполняться условие:

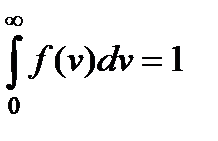(15)

Левая часть выражения (17.3) дает вероятность того, что молекула обладает скоростью в интервале от 0 до ∞. Поскольку скорость молекулы обязательно имеет какое-то значение, то указанная вероятность есть вероятность достоверного события и, следовательно, равна 1.

Функция распределения была найдена теоретически Максвеллом. Она имеет следующий вид:

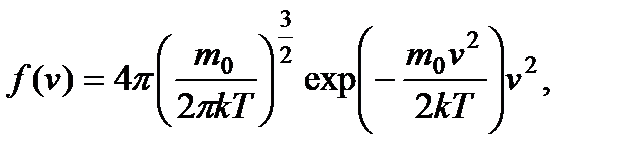(16)

где т₀ - масса молекулы.

Выражение (16) называется функцией распределения Максвелла.

Из (16) следует, что вид распределения молекул по скоростям зависит от природы газа (массы молекулы) и температуры Т. Давление и объем на распределение молекул по скоростям не влияют.

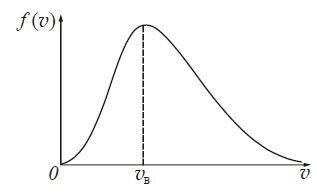
Рис.3. График функции распределения Максвелла

Схематичный график функции распределения Максвелла дан на рис. 3. Проведем анализ графика.

1. При скоростях стремящихся к нулю (v – >0) и к бесконечности (v –> ∞) функция распределения также стремится к нулю. Это означает, что очень большие и очень маленькие скорости молекул маловероятны.

2. Скорость v_B, отвечающая максимуму функции распределения, будет наиболее вероятной. Это означает, что основная часть молекул обладает скоростями близкими к вероятной.

Можно получить формулу для расчета наиболее вероятной скорости:

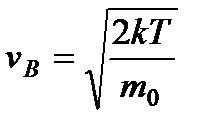(17)

где k — постоянная Больцмана; т₀ - масса молекулы.

3. В соответствии с условием нормировки (15) площадь, ограниченная кривой f(v) и осью абсцисс равна единице.

4. Кривая распределения имеет асимметричный характер. Это означает, что доля молекул, имеющих скорости больше наиболее вероятной, больше доли молекул, имеющих скорости меньше наиболее вероятной.

5. Вид кривой зависит от температуры и природы газа. На рис. 4 приведена функция распределения для одного и того же газа, находящегося при разных температурах. При нагревании максимум кривой понижается и смещается вправо, так как доля «быстрых» молекул возрастает, а доля «медленных» - уменьшается. Площадь под обеими кривыми остается постоянной и равной единице.

Установленный Максвеллом закон распределения молекул по скоростям и вытекающие из него следствия справедливы только для газа, находящегося в равновесном состоянии. Закон Максвелла — статистический, применять его можно только к большому числу частиц

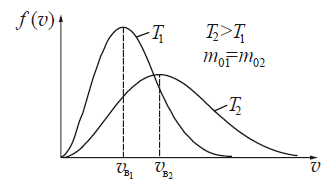
Рис. 4. Распределения Максвелла при разных температурах

Пользуясь функцией распределения Максвелла f(v), можно найти ряд средних величин, характеризующих состояние молекул.

Средняя арифметическая скорость – сумма скоростей всех молекул, деленная на число молекул:

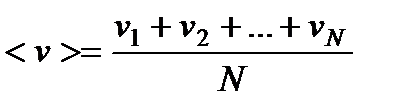. (18)

Средняя квадратичная скорость, определяющая среднюю кинетическую энергию молекул (см. формулу (10)), по определению равна

< v_КВ > = 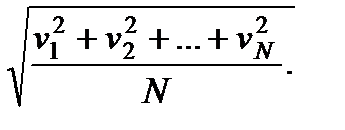(19)

Расчет с использованием распределения Максвелла дает следующие формулы:

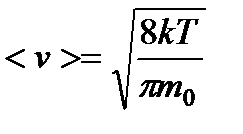(20)

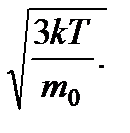< v_КВ > = (21)

Если учесть, что масса одной молекулы равна 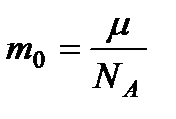, где μ – молярная масса; N_А – число Авогадро, а также то, что kN_A = R, то выражения для наиболее вероятной, средней арифметической и средней квадратичной скоростей можно переписать следующим образом:

<v_B> = 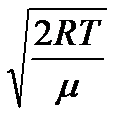; (22)

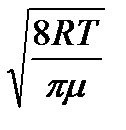= ; (23)

< v_КВ > = 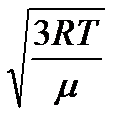. (24)

Сопоставляя (22), (23) и (24), можно заметить, что v_B,, < v_КВ > одинаково зависят от температуры газа и молярной массы, отличаясь только множителем. Их отношение выглядит следующим образом:

< v_В >: < v >: < v_КВ > = 1: 1,13: 1,22.