РАЗДЕЛ II. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕРМОДИНАМИКА.
ЯВЛЕНИЯ ПЕРЕНОСА. РЕАЛЬНЫЕ ГАЗЫ
Основные формулы для решения задач
Молекулярная физика
1. Количество вещества однородного газа (в молях):
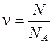 , или
, или 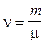 ,
,
где N - число молекул газа; 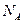 - число Авогадро; m - масса газа; m - молярная масса газа.
- число Авогадро; m - масса газа; m - молярная масса газа.
Если система представляет смесь нескольких газов, то количество вещества системы:
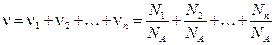 .
.
2. Молярная масса смеси газов:
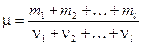 ,
,
где 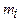 - масса i -го компонента смеси;
- масса i -го компонента смеси; 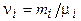 - количество вещества i -го компонента смеси; l - число компонентов смеси.
- количество вещества i -го компонента смеси; l - число компонентов смеси.
3. Концентрация молекул (число молекул в единице объема):
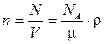 ,
,
где N - число молекул, содержащихся в объеме V; r - плотность вещества.
4. Основное уравнение молекулярно-кинетической теории идеального газа для давления:
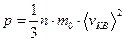 ,
,
где 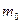 – масса молекулы,
– масса молекулы, 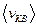 - средняя квадратическая скорость. Через энергию хаотического движения основное уравнение записывается в виде
- средняя квадратическая скорость. Через энергию хаотического движения основное уравнение записывается в виде
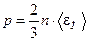 ,
,
где 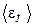 - средняя кинетическая энергия поступательного движения одной молекулы.
- средняя кинетическая энергия поступательного движения одной молекулы.
5. Средняя кинетическая энергия поступательного движения молекулы:
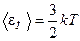 ,
,
где k - постоянная Больцмана, T - абсолютная температура.
6. Средняя полная кинетическая энергия одной молекулы
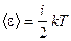 ,
,
где i - число степеней свободы молекулы.
7. Зависимость давления газа от концентрации молекул:
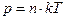 .
.
Статистика дает ответ на два основных вопроса: а) как распределены частицы макроскопических систем по координатам, скоростям, импульсам, энергиям и т.д.; б) как свойства таких систем связаны в условиях статистического равновесия с микрохарактеристиками отдельных частиц.
В основе классической статистики1) лежат следующие положения:
1) частицы, образующие макроскопические системы, различимы, их можно «метить», нумеровать. В принципе можно проследить за любой частицей;
2) физические характеристики частиц (скорость, импульс, энергия и т.д.) могут изменяться непрерывно, принимать любые значения;
3) в тождественных состояниях может находиться любое число частиц (любое число частиц может иметь одновременно одну и ту же скорость, одну и ту же энергию и т.п.).
В газах при наличии статистического равновесия господствует молекулярный хаос, обусловленный взаимодействием молекул при их столкновениях друг с другом и со стенками сосуда. В этом хаосе обнаруживаются отдельные закономерности, а именно - в отсутствии внешних силовых полей устанавливается равномерное распределение молекул по объему (в равных объемах - одинаковое число молекул), равномерное распределение скоростей и импульсов по направлениям (все направления равновероятны) и статистическое распределение скоростей и импульсов по модулю.
Распределение молекул по модулю скоростей
Из предположения о полной беспорядочности молекулярного движения следует, что скорости молекул газа могут принимать любые значения от 0 до  . Число возможных значений скорости в этом интервале бесконечно велико, а число молекул в любом реальном количестве газа конечно, то бессмысленно говорить о числе молекул, обладающих точно заданной скоростью, например, скоростью
. Число возможных значений скорости в этом интервале бесконечно велико, а число молекул в любом реальном количестве газа конечно, то бессмысленно говорить о числе молекул, обладающих точно заданной скоростью, например, скоростью 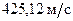 . Может случиться, что вообще ни одна молекула не обладает такой скоростью. Разумно поставить вопрос о числе молекул, обладающих скоростями, близкими к заданной, или о вероятности того, что данная молекула имеет скорость, лежащую в определенном интервале скоростей.
. Может случиться, что вообще ни одна молекула не обладает такой скоростью. Разумно поставить вопрос о числе молекул, обладающих скоростями, близкими к заданной, или о вероятности того, что данная молекула имеет скорость, лежащую в определенном интервале скоростей.
Обозначим через 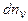 число молекул в единице объема газа, скорости которых лежат в интервале от v до
число молекул в единице объема газа, скорости которых лежат в интервале от v до 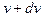 , через n - концентрацию молекул газа. Разделим
, через n - концентрацию молекул газа. Разделим 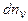 на
на 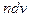 . Полученная величина является функцией v, т. е. зависит от того, в окрестности какой скорости v взят интервал
. Полученная величина является функцией v, т. е. зависит от того, в окрестности какой скорости v взят интервал 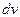 , так как возможные значения v не равновероятны:
, так как возможные значения v не равновероятны:
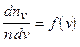 . (8.1)
. (8.1)
Функция (8.1), характеризующая распределение молекул (частиц) макроскопической системы по скоростям, есть плотность вероятности или функция распределения Максвелла.
Функция распределения Максвелла показывает, какова вероятность того, что скорость данной молекулы имеет значение, заключенное в единичном интервале скоростей, включающем данную скорость v, или каково относительное число молекул, скорости которых лежат в этом интервале.
Величина
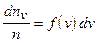 . (8.2)
. (8.2)
есть вероятность того, что скорость данной молекулы лежит в интервале от v до 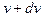 , или относительное число молекул, скорости которых заключены в этом интервале. Проинтегрировав (8.2) по v от 0 до ¥, мы получим вероятность того, что скорость данной молекулы принадлежит этому интервалу, или полное относительное число молекул. Очевидно,
, или относительное число молекул, скорости которых заключены в этом интервале. Проинтегрировав (8.2) по v от 0 до ¥, мы получим вероятность того, что скорость данной молекулы принадлежит этому интервалу, или полное относительное число молекул. Очевидно,
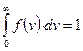 (8.3)
(8.3)
- это условие нормирования функции распределения Максвелла.
Функция распределения молекул по скоростям имеет вид
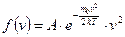 , (8.4)
, (8.4)
где 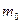 - масса молекулы; T - абсолютная температура газа; v - заданная скорость; А - константа, не зависящая от скорости и равная
- масса молекулы; T - абсолютная температура газа; v - заданная скорость; А - константа, не зависящая от скорости и равная
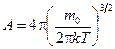 . (8.5)
. (8.5)
Таким образом,
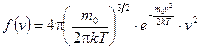 . (8.6)
. (8.6)
Распределение Максвелла (8.6) справедливо для частиц любых классических систем - газов, жидкостей, твердых тел.
Исследуем функцию распределения:
при 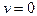
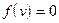 из-за множителя
из-за множителя 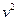 ,
,
при 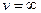
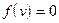 из-за множителя
из-за множителя 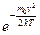 .
.
Таким образом, весьма малые и очень большие скорости маловероятны. При некотором v величина 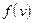 максимальна. Скорость
максимальна. Скорость 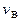 , соответствующая максимуму функции распределения, называется вероятнейшей
, соответствующая максимуму функции распределения, называется вероятнейшей
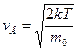 . (8.7)
. (8.7)
Максимальное значение функции распределения при данной температуре:
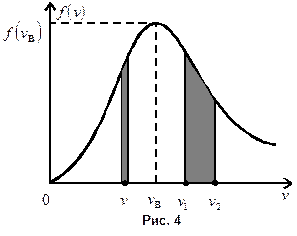 |
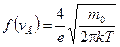 . (8.8)
. (8.8)
График функции распределения для некоторой температуры приведен на рис. 4. Узкая заштрихованная полоска на этом рисунке изображает вероятность того, что скорость данной молекулы принадлежит интервалу скоростей 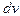 , взятому в окрестности v, или относительное число молекул, скорости которых лежат в этом интервале:
, взятому в окрестности v, или относительное число молекул, скорости которых лежат в этом интервале:
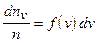 .
.
Площадь широкой полосы изображает вероятность того, что скорость данной молекулы имеет одно из значений в пределах от 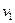 до
до 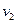 :
:
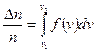 .
.
Вся площадь под кривой распределения численно равна вероятности того, что скорость данной молекулы имеет значение, принадлежащее интервалу 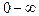 , или равна полному относительному числу молекул. Эта площадь равна единице.
, или равна полному относительному числу молекул. Эта площадь равна единице.
Кривая распределения асимметрична: ее нисходящая ветвь более полога. Площадь под кривой, лежащая правее максимума, больше площади, лежащей левее его. Значит, число молекул, скорости которых больше вероятнейшей, превышает число молекул, скорости которых меньше ее.
При повышении температуры максимум кривой распределения смещается в область б о льших скоростей, при этом «высота» максимума понижается; это видно из формул (8.7) и (8.8). Площадь же под кривой по-прежнему равна единице. Как видно из рис. 5, относительное число «медленных» молекул при повышении температуры уменьшается, а число «быстрых» возрастает.
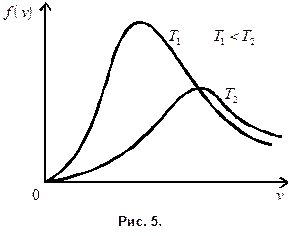 |
При 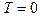 функция распределения для всех скоростей, кроме
функция распределения для всех скоростей, кроме 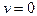 , тождественно равна нулю. Следовательно, при
, тождественно равна нулю. Следовательно, при 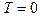 все молекулы должны покоиться.
все молекулы должны покоиться.
Число молекул в единице объема газа, скорости которых лежат в интервале от v до 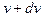 , равно
, равно
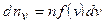 . (8.9)
. (8.9)
или после подстановки 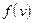
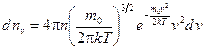 . (8.10)
. (8.10)
Это соотношение называется максвелловским законом распределения молекул по модулю скоростей.
От распределения молекул по скоростям перейдем к распределению молекул по энергиям поступательного движения. Для этого в (2.10) заменим переменную v переменной 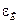 . Осуществив в (8.10) подстановку
. Осуществив в (8.10) подстановку 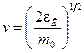 и
и  , получим
, получим
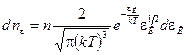 . (8.11)
. (8.11)
Вероятность того, что данная молекула обладает энергией, лежащей в единичном интервале, взятом в окрестности энергии 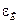 , или относительное число молекул, обладающих энергиями, заключенными в этом интервале, выражается соотношением
, или относительное число молекул, обладающих энергиями, заключенными в этом интервале, выражается соотношением
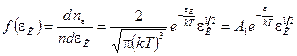 , (8.12)
, (8.12)
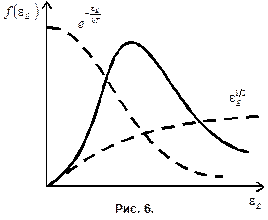 где
где 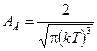 .
.
На рис. 6 изображена кривая функции распределения молекул по энергиям.
Зная распределение энергий по скоростям и энергиям можно найти целый ряд средних величин, характеризующих молекулы.
Средняя скорость. Проинтегрировав  по v от нуля до бесконечности и разделив найденную сумму на полное число молекул n, найдем
по v от нуля до бесконечности и разделив найденную сумму на полное число молекул n, найдем  :
:
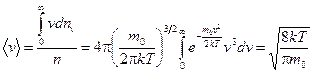 . 8.13)
. 8.13)
Представим (8.13) следующим образом:
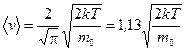 .
.
Учтем, что 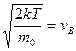 - вероятнейшая скорость. Таким образом,
- вероятнейшая скорость. Таким образом,
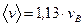 . (8.14)
. (8.14)
Средняя скорость на 13% больше вероятнейшей скорости.
Масса одной молекулы равна
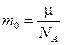 , (8.15)
, (8.15)
где m - молярная масса; 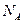 - число Авогадро.
- число Авогадро.
Подставив (8.15) и (8.13) и учитывая, что 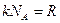 , получим для средней скорости
, получим для средней скорости
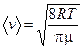 . (8.16)
. (8.16)
Средняя кинетическая энергия поступательного движения молекул равна
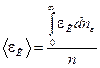 .
.
Подставив в это выражение 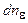 по (8.11), получим
по (8.11), получим
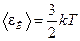 . (8.17)
. (8.17)
Средняя квадратическая скорость равна корню квадратному из среднего квадрата скоростей молекул:
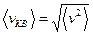 .
.
Найдем среднюю квадратическую скорость, воспользовавшись (8.17)
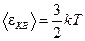 или
или 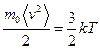 ,
,
откуда 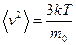 . Следовательно,
. Следовательно,
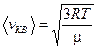 . (8.18)
. (8.18)
Средняя квадратичная скорость на 22% больше вероятнейшей.
9. Уравнение Менделеева-Клапейрона
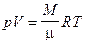 ,
,
где R - универсальная газовая постоянная, M - масса системы.
10. Газовые законы:
а) закон Бойля-Мариотта (изотермический процесс 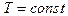 ,
, 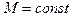 ):
):
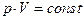 ;
;
б) закон Гей-Люссака (изобарический процесс 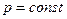 ,
, 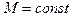 ):
):
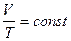 ;
;
в) закон Шарля (изохорический процесс 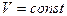 ,
, 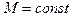 ):
):
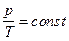 ;
;
г) уравнение Пуассона (адиабатический процесс 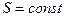 ,
, 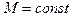 ):
):
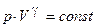 ,
, 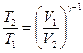 ,
, 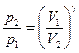 ;
; 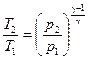 .
.
где 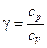 - показатель адиабаты, S - энтропия системы.
- показатель адиабаты, S - энтропия системы.
11. Удельные теплоемкости газа при постоянном объеме 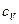 и при постоянном давлении
и при постоянном давлении 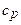 :
:
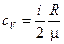 ;
; 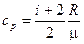 .
.
12. Связь между удельной c и молярной (C) теплоемкостями:
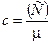 ,
, 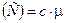 .
.
13. Уравнение Роберта Майера:
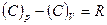 .
.
 2015-01-21
2015-01-21 4966
4966







