Пусть дана функция y = f (x), определенная на множестве значений аргумента, содержащего некоторую точку а. Рассмотрим 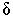 -окрестность точки а, где
-окрестность точки а, где 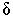 - малое положительное число
- малое положительное число 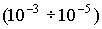 :
:
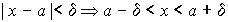 .
.
Пусть для значений x, достаточно близких к а, т. е. принадлежащих d -окрестности точки а, соответствующие значения функции y = f (x) неограниченно приближаются к некоторому числу А. Это значит, что разность (f (x) - A) все время уменьшается. В этом случае число А называется пределом функции y = f (x) при 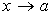 .
.
О п р е д е л е н и е 1. Число А называется пределом функции y = f (x) при 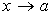 , если для любого сколь угодно малого e найдется малое положительное
, если для любого сколь угодно малого e найдется малое положительное 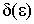 , такое, что для всех значений х, удовлетворяющих неравенству
, такое, что для всех значений х, удовлетворяющих неравенству 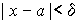 будет выполняться неравенство
будет выполняться неравенство 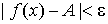 (рис. 63):
(рис. 63):
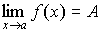 . (4.2)
. (4.2)
Неравенство 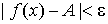 означает, что значения функции y = f (x) попадают в e -окрестность точки А на оси ОУ.
означает, что значения функции y = f (x) попадают в e -окрестность точки А на оси ОУ.
Из рис. 63 следует, что, если число А есть предел функции y = f (x) при 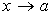 , то как только значения независимой переменной х попадут в , то как только значения независимой переменной х попадут в 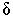 -окрестность точки а, так сразу соответствующие значения функции попадут в -окрестность точки а, так сразу соответствующие значения функции попадут в 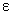 -окрестность точки А, т. е. график функции будет целиком лежать в полосе шириной 2e. -окрестность точки А, т. е. график функции будет целиком лежать в полосе шириной 2e.
| 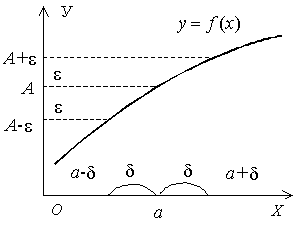 Рис. 63
Рис. 63
|
О п р е д е л е н и е 2. Число А называется пределом функции y = f (x) при 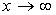 , если для всякого положительного сколь угодно малого e найдется такое положительное число , если для всякого положительного сколь угодно малого e найдется такое положительное число 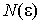 , что для всех значений х, удовлетворяющих условию , что для всех значений х, удовлетворяющих условию 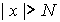 , будет выполняться неравенство , будет выполняться неравенство 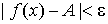 (рис. 64). (рис. 64).
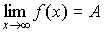 (4.3) (4.3)
| 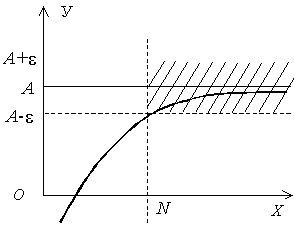 Рис. 64
Рис. 64
|
 2015-01-21
2015-01-21 444
444







