Решение систем линейных уравнений методом Крамера

Пусть нам требуется решить систему линейных алгебраических уравнений

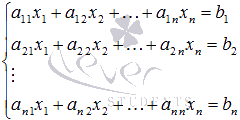
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .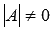

Пусть 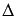- определитель основной матрицы системы, а 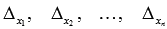- определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

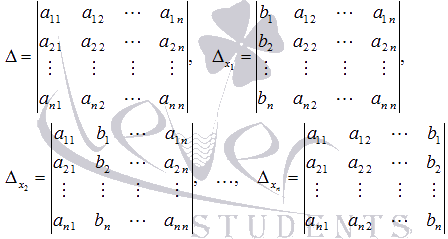
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как 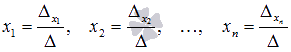. Так находится решение системы линейных алгебраических уравнений методом Крамера.

Пример.

Решите систему линейных уравнений методом Крамера .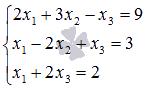

Решение.

Основная матрица системы имеет вид 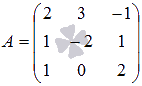. Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения):

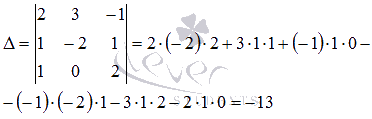
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.

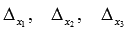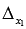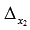Составим и вычислим необходимые определители (определитель получаем, заменив в матрице А первый столбец на столбец свободных членов , определитель - заменив второй столбец на столбец свободных членов, 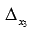- заменив третий столбец матрицы А на столбец свободных членов):

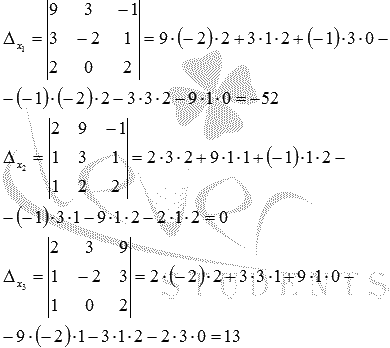
Находим неизвестные переменные по формулам :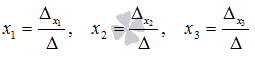

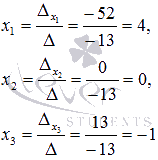
Ответ:

x₁ = 4, x₂ = 0, x₃ = -1.

Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.