Арифметическое свойство придела

Арифметические свойства предела функции.
Пусть функции f и g определены на интервале (a, b), кроме быть может точки x ₀. Если существует пределы

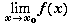^{и ,}

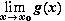то существуют пределы в левых частях равенств и имеют место эти равенства:

^a.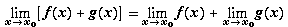
б.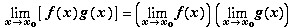

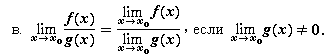
Эти свойства вытекают из определения Гейне предела функции и соответствующих свойств сходящихся последовательностей.
2. Если

^,

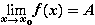^{то существует проколатая окрестность точки , где функция f (x) ограничена.}
Действительно, если взять = 1 0, то из существования конечного предела следует, что существует 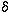0, что для всех x: 0 | x - x ₀ | 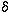, выполняется | f (x) - A | 1, отсюда, | f (x) | - | A | | f (x) - A | 1, т.е.

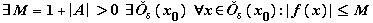
3. Если

^,

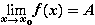^{то существует проколотая окрестность 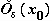точки 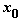, что для всех x :}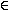

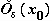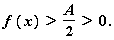
Действительно, возьмем 0, тогда из существования конечного предела, следует, что существует
^{окрестность 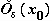, что для всех x :}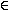

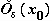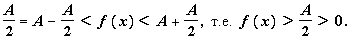
4. Свойства, связанные с неравенствами.
Если

^,

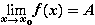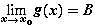
^{и для всех x 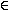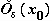: f (x) 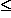g (x), то A 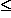B}
Если

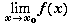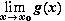^{= = A}

и для всех x 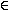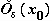: 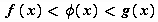, то существует

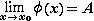
Доказательства этих свойств следуют из следующих свойств для сходящихся последовательностей и определения предела функции по Гейне.