или в другой записи
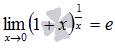
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность 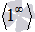 .
.
Разберем несколько примеров нахождения предела по второму замечательному пределу с подробным оприсанием решения.
Пример.
Вычислить предел 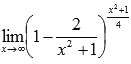
Решение.
Подставляем бесконечность:
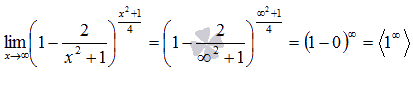
Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела.
Сделаем замену переменных. Пусть
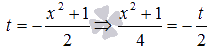
Если 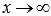 , то
, то 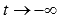
Исходный предел после замены примет вид:
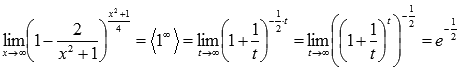
Ответ:
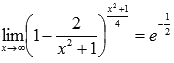
Пример.
Вычислить предел 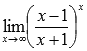
Решение.
Подставляем бесконечность:
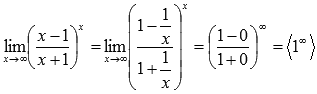
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
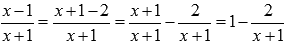
Тогда предел запишется в виде:
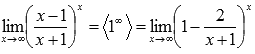
Сделаем замену переменных. Пусть
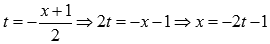
Если 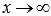 , то
, то 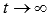
Исходный предел после замены примет вид:
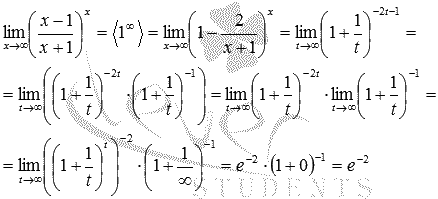
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:

Пример.
Вычислить предел 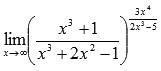
Решение.
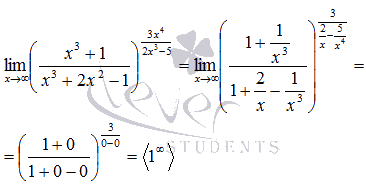
Преобразуем функцию, чтобы применить второй замечательный предел:
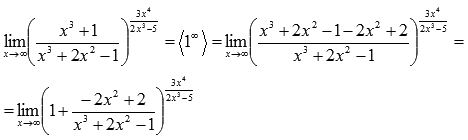
Сейчас домножим показатель на 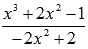 и разделим на это же выражение, затем используем свойства степени:
и разделим на это же выражение, затем используем свойства степени:
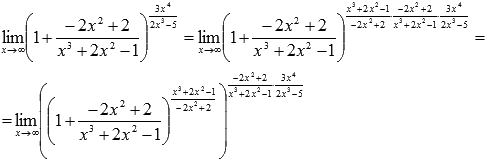
Так как показатели степени числителя и знаменателя дроби 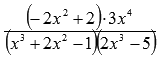 одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях (см. непосредственное вычисление пределов):
одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях (см. непосредственное вычисление пределов):

Если произвести замену  , то получим второй замечательный предел в чистом виде, следовательно,
, то получим второй замечательный предел в чистом виде, следовательно,
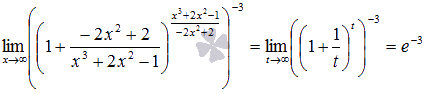
Ответ:
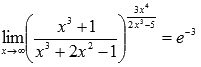
 2015-01-21
2015-01-21 1735
1735








