Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Первый замечательный предел имеет вид: 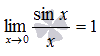
На практике чаще встречаются модификации первого замечательного предела в виде
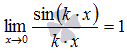
где, k – коэффициент.
Пояснение:
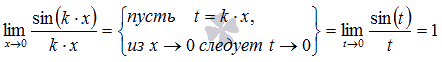
Следствия первого замечательного предела:
1. 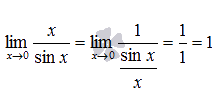
2. 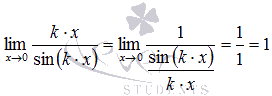
Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.
Разберем несколько примеров нахождения предела по первому замечательному пределу с подробным оприсанием решения.
Пример.
Найти предел не пользуясь правилом Лопиталя 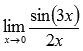
Решение.
Подставляем значение:
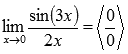
Пришли к неопределенности ноль делить на ноль. Смотрим в таблицу неопределенностей для определения метода решения. Комбинация синуса и его аргумента подсказывает нам о применении первого замечательного предела, но для этого сначала нужно немного преобразовать выражение. Домножим на 3х и числитель и знаменатель дроби.
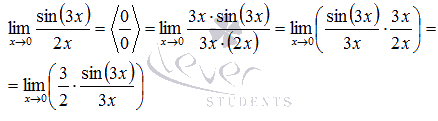
В силу следствия из первого замечательного предела 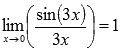 , поэтому приходим к результату:
, поэтому приходим к результату:
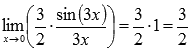
Ответ:
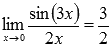
Пример.
Вычислить предел 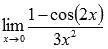
Решение.
Подставляем значение:
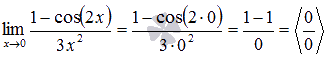
Пришли к неопределенности ноль делить на ноль. Преобразуем числитель, используя формулы тригонометрии.
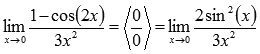
Стало видно, что здесь можно применить первый замечательный предел:
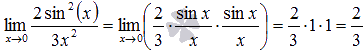
Ответ:
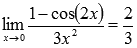
Пример.
Вычислить предел 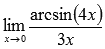
Решение.
Подставляем значение:
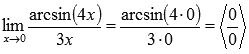
Пришли к неопределенности ноль делить на ноль. Сделаем замену.
Пусть
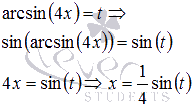
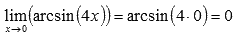 , следовательно,
, следовательно, 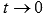 при
при 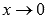 .
.
Тогда предел после замены переменной примет вид:
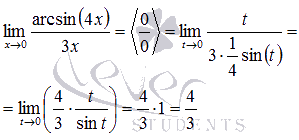
Ответ:
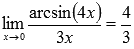
предел имеет вид:
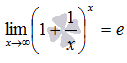
 2015-01-21
2015-01-21 9215
9215
