Следствие. Доказать непрерывность функции в точке

ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ.

Пример.

Доказать непрерывность функции 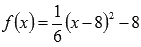в точке .

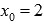Решение.

Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов 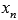, сходящуюся к 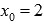, причем 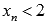. Примером такой последовательности может являться

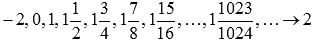
Соответствующая последовательность значений функции будет иметь вид

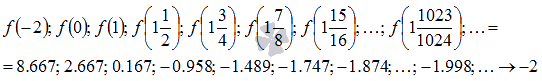
На рисунке соответствующие значения показаны зелеными точками.

Легко видеть, что эта последовательность сходится к -2, поэтому .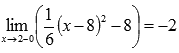

Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов 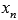, сходящуюся к 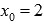, причем 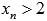. Примером такой последовательности может являться

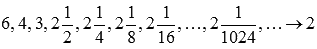
Соответствующая последовательность значений функции будет иметь вид

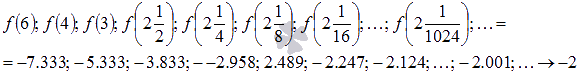
На рисунке соответствующие значения показаны синими точками.

Легко видеть, что эта последовательность также сходится к -2, поэтому .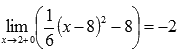

Этим мы показали, что пределы слева и справа равны, следовательно, существует предел функции 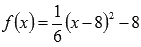в точке 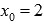, причем

Вычислив значение функции в точке 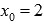можно говорить о выполнении равенства 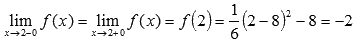, это доказывает непрерывность исходной функции в точке.