2015-01-21
646
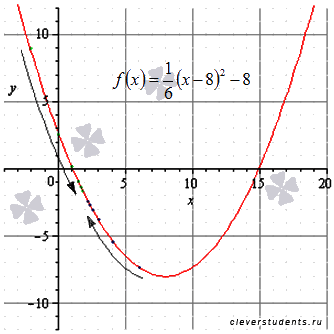
Определение устранимого разрыва первого рода.
В точке 
функция имеет устранимый разрыв первого рода, если предел слева равен пределу справа, но они не равны значению функции в точке,то есть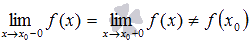 
.
Пример.
Найти точки разрыва функции и определить их тип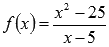 
.
Решение.
Найдем область определения функции:
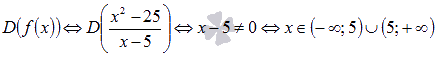
Точкой разрыва нашей функции может быть только граничная точка области определения, то есть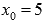 
. Проверим функцию на непрерывность в этой точке.
На области определения выражение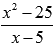 
можно упростить:
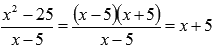
Находим пределы слева и справа. Так как функция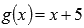 
непрерывна при любом действительном х, то
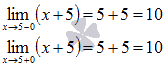
Следовательно, пределы слева и справа равны, а сама функция 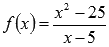в точке 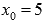не определена, поэтому, в точке 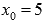функция имеет устранимый разрыв первого рода.
Определение неустранимого разрыва первого рода (точка скачка функции).
В точке функция имеет неустранимый разрыв первого рода, если пределы слева и справа НЕ равны, то есть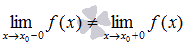 
. Точку в этом случае называют точкой скачка функции.
Пример.
Исследовать кусочно-непрерывную функцию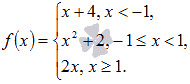 
на непрерывность, определить вид точек разрыва, сделать чертеж.
Решение.
Разрывы могут быть лишь в точках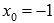 
или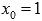 
.
Найдем пределы слева и справа от этих точек, а также значения исходной функции в этих точках.
Слева от точки 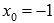наша функция есть 
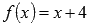и в силу непрерывности линейной функции 
.
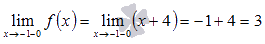В самой точке 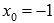наша функция есть 
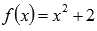, поэтому 
.
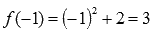На промежутке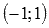 
наша функция есть 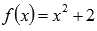и в силу непрерывности квадратичной функции
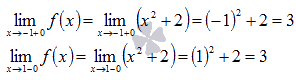
В точке 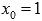наша функция есть 
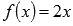, поэтому 
.
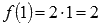Справа от 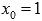наша функция есть 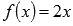и в силу непрерывности линейной функции
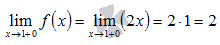
В итоге имеем:
· 
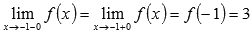следовательно, в точке 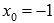исходная кусочная функция непрерывна,
· 
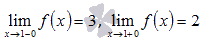, то есть 
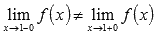, следовательно, в точке 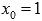неустранимый разрыв первого рода (скачок).
