Важнейшим понятием теории вероятностей является понятие случайной величины.
Случайной величиной Х называется числовая функция, заданная на множестве событий.
Случайная величина это такаявеличина, которая в результате опыта принимает одно из множества всевозможных значений и до опыта невозможно узнать, какое из значений она примет.
Случайные величины обозначаются большими буквами Х,Y,Z,..., их возможные значения - маленькими (х, y,...) или x,h,.... Будем пользоваться сокращением с.в. - случайная величина.
Пусть (W, F, Р) - вероятностная модель некоторого эксперимента с конечным числом исходов, N(W)<¥, и алгеброй F всех подмножеств W, В рассмотренных ранее примерах нас интересовал подсчёт вероятностей событий АÎF, природа пространства элементарных событий W нас не интересовала. Случайная величина:(вводимое понятие) это та величина, которая подлежит “измерению” в случайных экспериментах.
С каждым возможным исходом опыта (элементарным событием) можно связать одно и только одно из возможных значений случайной величины.
Определение1: Всякая числовая функция Х=Х(w), определённая на (конечном) пространстве элементарных событий W, называется случайной величиной.
Пример1. В модели двукратного подбрасывания монеты (монета подбрасывается 2 раза) с пространством исходов W=(гг, гр, рг, рр) определим случайную величину Х(w) - число выпавших гербов с помощью таблицы:
| w | гг | гр | рг | рр |
| Х(w) |
Здесь Х=Х(w) по своему смыслу число гербов, отвечающих исходу w.
Определение2. Случайной величиной Х, заданной на вероятностном пространстве (w, F, Р) называется измеримая функция Х=Х(w), отображающая пространство элементарных событий W в множество действительных чисел 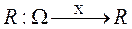
Измеримость функции Х=Х(w) позволяет любому борелевскому множеству Bх поставить в соответствие множество А в пространстве W, АÎF.
Поэтому можно вычислить:
Р(Х(w)ÎBх)=Р(ХÎBх)=Р(А) (1)
В отличие от функций в математическом анализе в теории вероятностей не интересуются, каким образом W отображается в R. Для ТВ важно задать множество возможных значений Х и распределение на этом множестве вероятностей (1). Формула (1) описывает распределение вероятностей попадания случайной величины в подмножество Bх. Случайная величина считается заданной, если задана область её возможных значений и распределение вероятностей (1) (закон распределения вероятностей).
Случайные величины и их законы распределения
Примеры случайных величин.
1). Опыт - бросание игральной кости - случайная величина Х - число выпавших очков, множество возможных значений: В={1, 2, 3, 4, 5, 6}- счётно и конечно.
2). Опыт - работа машины после ремонта; случайная величина Т - время наработки машины до первого отказа (сбоя). Множество возможных значений В - теоретически вся правая половина оси абсцисс 0t, включая и 0: { t³0 }. Этот участок ограничен справа, но граница расплывчата, неопределённа. Множество В в этом случае несчётно.
3). Опыт - ведётся тестирование изделий до появления первого исправного изделия. Случайная величина Y - число тестов, которое будет произведено. Множество возможных значений B ={1,2,...,n,...} бесконечно, но счётно.
4). Опыт - измерение сопротивления линии. Результат округляется до ближайшего целого значения. Случайная величина Х - ошибка от округления. Множество возможных значений В - участок числовой оси от -1 до +1 включая концы, т.е. В ={[-1,+1]}; оно несчётно.
Из примеров видно, что случайные величины бывают двух типов: у одних множество В конечно или счётно (их можно перенумеровать в каком-то порядке; примеры 1,3). У других это множество сплошь занимает какой-то участок числовой оси, границы которого могут быть как зафиксированными (пример 4), так и неопределёнными (пример 2), а множество возможных значений несчётно. Случайные величины первого типа называются дискретными, а второго – непрерывными.
Дискретной случайной величиной называется случайная величина с конечным или счётным множеством возможных значений.
Непрерывной случайной величиной называется случайная величина, множество значений которой является непрерывным множеством.
Закон распределения. Законом распределения случайной величины называется любое правило (таблица, функция), позволяющая находить вероятности всевозможных событий, связанных со случайной величиной (например, вероятность того, что она примет какое-то значение или попадёт на какой-нибудь интервал). Если случайная величина Х имеет данный закон распределения, то про неё говорят, что она “распределена” по этому закону (или “подчинена” этому закону).
Наиболее простую форму можно придать закону распределения дискретной случайной величины. Для этого перечисляются возможные значения случайной величины Х: х1, х2,..., хn,... и соответствующие им вероятности.
Рядом распределения дискретной случайной величины Х называется таблица, в верхней строке которой перечислены в порядке возрастания все возможные значения случайной величины Х: х1, х2 ,..., хn,..., а в нижней - вероятности этих значений: р1, р2,..., рn,..., где рi=P{X=xi} - вероятность того, что в результате опыта случайная величина Х примет значение хi (i=1, 2,..., n,...).
Ряд распределения случайной величины Х записывается в виде таблицы:
Х: (1)
| x1 | x2 | ... | xn | ... |
| p1 | p2 | ... | pn | ... |
Т.к. события {X=x1}, {X=x2},... несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке ряда (1), равна единице:
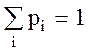 (2)
(2)
Эта единица как-то распределена между значениями случайной величины.
Пример 1: Рассматривается работа трёх независимо работающих технических устройств (ТУ); вероятность нормальной работы первого ТУ равна 0.2; второго - 0.4; третьего - 0.5; случайная величина Х - число работающих ТУ. Построить ряд распределения случайной величины Х.
Решение. Возможные значения случайной величины Х: 0, 1, 2, 3. Соответствующие им вероятности найдём, пользуясь правилами сложения и умножения Нормальную работу обозначим знаком “+”, а отказ - знаком “-”.
р1 =Р{X=0}=P{- - -}=0.8*0.6*0.5=0.24
р2 =P{X=1}=P{+ - -}+P{- + -}+P{- -+}=
=0.2*0.6*0.5+0.8*0.4*0.5+0.8*0.6*0.5= =0.46
р3 =Р{X=2}=P{- + +}+P{+ - +}+P{+ + -}=
=0.8*0.4*0.5+0.2*0.6*0.5+0.2*0.4*0.5==0.26
p4 =P{X=3}=P{+ + +}=0.2*0.4*0.5=0.04
Как и следовало ожидать
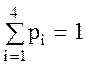 .
.
Ряд распределения случайной величины Х имеет вид:
Х:
| 0.24 | 0.46 | 0.26 | 0.04 |
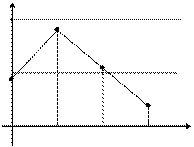
Графическое изображение ряда распределения называется многоугольником распределения.
 pi
pi
0.5
0.25
....0 1 2 3 xi
Рис.1. Многоугольник распределения (к примеру 1).
Строится он так: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения случайной величины. Полученные точки для наглядности (только для наглядности!) соединяются отрезками прямых.
 2015-01-21
2015-01-21 1978
1978
