Основные свойства математических ожиданий

1. Для любой константы С имеем свойства, которые вытекают из определения мат. ожидания:

а) M[CX]=CM[X];

b) M[C]=C

2. Если а и b постоянные, то M[a+bX]=a+bM[X].

3. Аддитивность: M[X+Y]=M[X]+M[Y]

Доказательство: Из определения M[X+Y] для дискретной случайной величины получаем:

M[X+Y]= 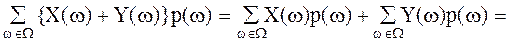M[X]+M[Y].

Из этого свойства нетрудно вывести по индукции свойство конечной аддитивности мат.ожидания:

M[X₁+...+X_n]=M[X₁]+...+M[X_n]

4. Математическое ожидание произведения двух независимых случайных величин равно произведению их мат. ожиданий

M[X Y] =M[X] M[Y]

Это свойство допускает обобщение на произведение любого числа независимых сомножителей

M[X₁ X_n ]=M[X₁]_....... M[X_n]

Помимо математического ожидания в теории вероятностей применяются и другие характеристики положения: мода и медиана случайной величины.

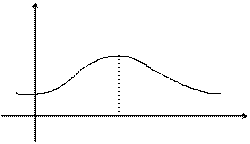Модой случайной величины называется её наиболее вероятное значение (то, для которого вероятность р_i или плотность распределения f(х) достигает максимума).

f(х)

M_x- мода х

Рис.1

На рис.1 показана кривая распределения случайной величины Х; точка, в которой плотность f(x) достигает максимума и есть мода M_x. Если вероятность и плотность достигают максимума в нескольких точках - распределение называют полимодальным.

Медиана – характеристика положения для непрерывной случайной величины. Медианой непрерывной случайной величины X называется такое ее значение x_m, для которого P{X<x_m}=P{X>x_m}=1/2, т.е. одинаково вероятно окажется ли случайная величина меньше или больше x_m.

Геометрическая медиана - это абсцисса той точки на оси Ох, для которой площади справа и слева равны.