Решение системы трех линейных алгебраических уравнений при помощи обратной матрицы

Присоединенной (союзной) матрицей к квадратной матрице

А= 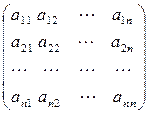называется матрица

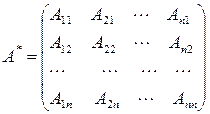, (31)

где 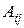– алгебраические дополнения элементов 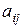определителя матрицы А.

Матрица 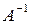называется обратной к квадратной матрице А, если выполнено условие: 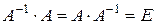, где Е – единичная матрица той же размерности, что и А.

Обратная матрица существует тогда и только тогда, когда квадратная матрица А – невырожденная, т.е. .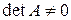

Чтобы найти обратную матрицу 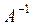, необходимо:

а) проверить невырожденность матрицы А, вычислив определитель det A;

б) найти союзную матрицу А ^* к матрице А;

в) найти обратную матрицу по формуле:

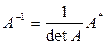. (32)

Если систему линейных алгебраических уравнений(28) переписать в матричном виде AX = B, то ее решение можно получить матричным способом, т.е. при помощи обратной матрицы:

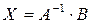, (33)

где 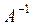– обратная матрица для данной матрицы А.