Умножение матрицы A на число k:
B = k × A = 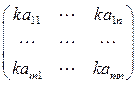 ,
,
или, в краткой записи:
B = k × A Û bij = k × aij (i = 1,2,…, m; j = 1,2,…, n). (21)
Сложение (вычитание) матриц A и B одинаковой размерности:
Cm´n = Am´n ± Bm´n Û cij = aij ± bij (i = 1,2,…, m; j = 1,2,…, n). (22)
Произведение матриц Am´n и Bn´k:
Cm´k = Am´n × Bn´k 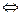
cij = ai1b1j + ai2b2j + ¼ + ainbnj (i = 1,2,…, m; j = 1,2,…, k). (23)
Формулу (23) легко запомнить, как правило умножения «строка на столбец»: произведение матриц Am´n и Bn´k есть матрица Cm´k, у которой элемент cij равен сумме произведений соответствующих элементов i- й строки матрицы A и j- го столбца матрицы В.
Замечание. Перемножать можно только соответственные матрицы А и В, т.е.число столбцов матрицы А должно быть равно числу строк матрицы В.
Если задан многочлен 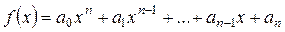 , то матричным многочленом
, то матричным многочленом 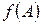 называется выражение
называется выражение
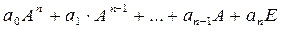 ,
,
где А – квадратная матрица, 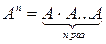 и Е – единичная матрица той же размерности, что и А. Значением матричного многочлена является матрица.
и Е – единичная матрица той же размерности, что и А. Значением матричного многочлена является матрица.
 2015-01-21
2015-01-21 379
379








