2015-01-21
835
Пусть функция y= f(x) задана на (a, b) и x 0 (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x 0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значений f(x) в окрестности точки x 0 можно заменить более легкой задачей вычисления значений P(x).
Пусть искомый многочлен имеет степень n P(x) = P n (x). Будем искать его в виде
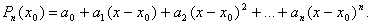 | (1) |
В этом равенстве нам нужно найти коэффициенты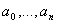 
.
Для того чтобы этот многочлен был "близок" к функции f(x) потребуем выполнения следующих равенств:
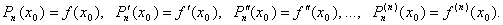
Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты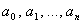 
многочлена P n(x) исходя из условия равенства производных.
Введем обозначение n! = 1·2·3… n, 0! = 1, 1! = 1.
Подставим в (1) x = x 0 и найдем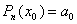 
, но с другой стороны 
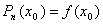. Поэтому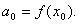 
Далее найдем производную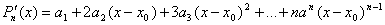 
и вычислим 
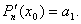Следовательно, 
.
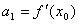Учитывая третье условие и то, что
,
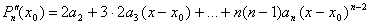получим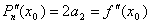 
, т.е. 
.
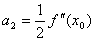Далее 
. Значит,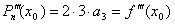 
, т.е. 
.
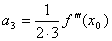Очевидно, что и для всех последующих коэффициентов будет верна формула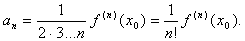 
Подставляя найденные значения коэффициентов 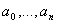в формулу (1), получим искомый многочлен:
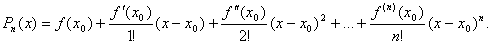
Обозначим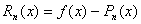 
и назовем эту разность n -ым остаточным членом функции f(x) в точке x 0. Отсюда 
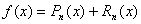и, следовательно, 
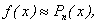если остаточный член будет мал.
Оказывается, что если x0 (a, b) при всех x (a, b) существует производная f (n+1)(x), то для произвольной точки x (a, b) существует точка, лежащая между x 0 и x такая, что остаток можно представить в виде:
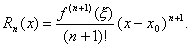
Это так называемая формула Лагранжа для остаточного члена.
Формула
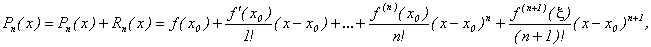где x (x 0, x) называется формулой Тейлора.
Если в этой формуле положить x 0 = 0, то она запишется в виде
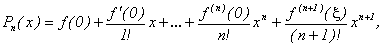
где x (x 0, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.
.
