Производные от состава используются при расчете дифференциальных свойств ТС.
Из выражения: 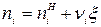 , (1)
, (1)
следует, что 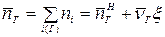 , (2)
, (2)
где 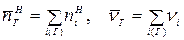 .
.
После дифференцирования (1) и (2) имеем:
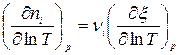 , (3)
, (3)
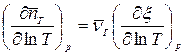 , (4)
, (4)
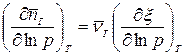 . (5)
. (5)
Закон действующих масс имеет вид:
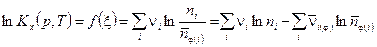
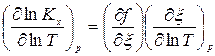 . Тогда
. Тогда 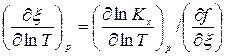 .
.
Учитывая, что 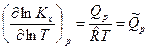 , получим соотношение для производной пробега ХР
, получим соотношение для производной пробега ХР 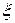 по ln T:
по ln T:
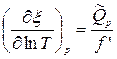 . (6)
. (6)
Соотношение для производной пробега ХР 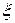 по давлению определяется аналогично, учитывая, что
по давлению определяется аналогично, учитывая, что
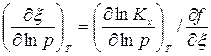 , а
, а 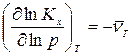 .
.
Тогда получим: 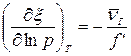 , (7)
, (7)
где производная 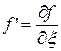 равна
равна
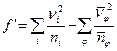 , (8)
, (8)
где 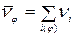 ;
; 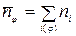 .
.
Соотношение (8) можно получить, используя «цепное правило» дифференцирования, из выражения
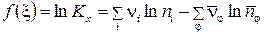 .
.
Обозначим 1ое слагаемое 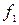 , а второе -
, а второе - 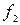 . Тогда
. Тогда
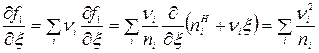
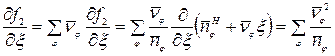 ,
,
где 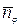 - суммарное количество веществ в
- суммарное количество веществ в 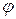 -ой фазе;
-ой фазе; 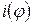 - список веществ в фазе с номером
- список веществ в фазе с номером 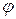 ;
; 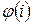 - номер фазы, где находится i -ое вещество.
- номер фазы, где находится i -ое вещество.
 2015-01-21
2015-01-21 424
424








