Рассмотрим ТС, в которой присутствуют кс – веществ в различных агрегатных состояниях, распределенных по кf фазам. Искомыми величинами являются:
1. Величины, определяющие состав ТС (количества веществ: n 1, n 2, …, ni, …, nкс, моль. или молярные доли х 1, х 2, …, хi, …, xкс, i =1, 2, …, кс и количество веществ в фазах: 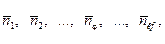 моль,
моль, 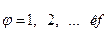 ). При этом
). При этом 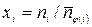 , где
, где 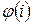 - номер фазы, где находится i -ое вещество, а
- номер фазы, где находится i -ое вещество, а 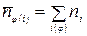 где
где 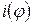 - список веществ в фазе
- список веществ в фазе 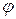 .
.
2. Молярные свободные энергии Гиббса атомов химических элементов, находящихся в ТС: 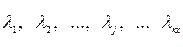 , где j =1, 2, …, кх. Индекс кх означает число химических элементов, присутствующих во всех соединениях термодинамической системы. При этом в расчете используются химические реакции распада веществ системы на атомы.
, где j =1, 2, …, кх. Индекс кх означает число химических элементов, присутствующих во всех соединениях термодинамической системы. При этом в расчете используются химические реакции распада веществ системы на атомы.
3. Температура и давление, или 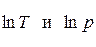 . Для нахождения неизвестных величин решается СУХР:
. Для нахождения неизвестных величин решается СУХР:
СУХР= 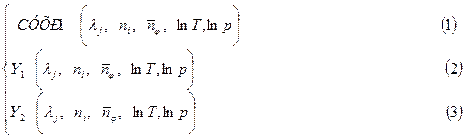
В качестве уравнений (2) и (3) используются уравнения баланса заданных независимых параметров, которые были рассмотрены нами ранее. Система уравнений (1) –(3) решается методом Ньютона или методом простой итерации. В СУХР1 для ТС с произвольным числом ХР входят:
- уравнения нормировки,
- уравнения материального баланса,
- уравнения химического равновесия химических реакций распада веществ системы на атомы.
Последовательность решения задачи:
1. Решается СУХР (1)-(3) и находится состав, давление и температура.
2. Определяются производные от состава с помощью СУХР1.
3. Рассчитываются интегральные и дифференциальные свойства ТС.
Рассмотрим уравнения, входящие в СУХР 1.
1. Уравнение нормировки записывается в виде положения, что количество веществ в j -ой фазе равно:
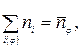 (4)
(4)
или 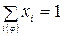 , (5)
, (5)
где i(φ) – список веществ, входящих в φ- ую фазу; φ =1, 2, …. кf.
Число уравнений нормировки равно числу фаз термодинамической системы кf.
2. Уравнение материального баланса (УМБ). В случае протекания химических реакций в закрытых термодинамических системах для каждого химического элемента суммарное число атомов, входящих во все вещества системы, является величиной постоянной. Тогда для каждого химического элемента j имеем уравнение материального баланса в виде
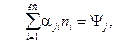 (6)
(6)
где j =1, 2,…, кх, i =1, 2,…, кс, αji –число атомов j –го химического элемента в молекуле i – го вещества; Ψj - материальная постоянная, равная числу молей атомов j –го химического элемента во всех соединениях закрытой термодинамической системы, [моль].
Число уравнений материального баланса равно числу различных химических элементов (ХЭ), присутствующих в ТС-кх.
Набор коэффициентов αji для всех веществ системыобразует матрицу размером кх · кс:
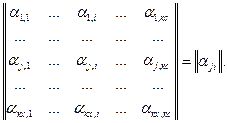
Суммарное количество вещества 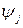 во всех соединениях закрытой системы при протекании ХР можно представить также в виде:
во всех соединениях закрытой системы при протекании ХР можно представить также в виде:
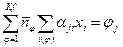 ,
, 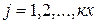 . (7)
. (7)
Уравнения (6), (7) можно записать в матричной форме: 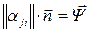 ,
,
где вектор 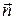 - набор ni, i=1, 2, …, кс; вектор
- набор ni, i=1, 2, …, кс; вектор 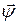 - набор материальных постоянных
- набор материальных постоянных 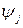 , j= 1, 2, …, кх.
, j= 1, 2, …, кх.
4. Уравнения химического равновесия (УХР). Для получения УХР удобно использовать уравнения химических реакций распада на атомы веществ, присутствующих в термодинамической системе:
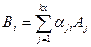 , где
, где 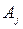 - символ j-го атома,
- символ j-го атома, 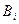 - символ i-го вещества.
- символ i-го вещества.
Условие равенства нулю химического сродства этой химической реакции в момент равновесия примет вид:
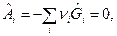 или:
или: 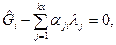 (8)
(8)
где 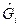 - мольная свободная энергия Гиббса i –го вещества (для левой части уравнения ХР распада вещества
- мольная свободная энергия Гиббса i –го вещества (для левой части уравнения ХР распада вещества 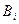 ); λj – мольная свободная энергия Гиббса атомов j –го химического элемента (для правой части уравнения ХР распада веществ
); λj – мольная свободная энергия Гиббса атомов j –го химического элемента (для правой части уравнения ХР распада веществ 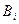 ),
), 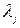 является искомой величиной, наряду с составом ТС.
является искомой величиной, наряду с составом ТС.
Для многофазной системы (газа и конденсата) имеем:
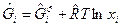 , (9)
, (9)
где 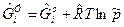 - для газа;
- для газа; 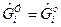 - для конденсата.
- для конденсата.
После подстановки (9) в (8) получим:
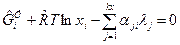 . (10)
. (10)
Обозначим безразмерные величины 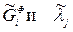 :
: 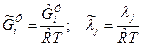 . Тогда
. Тогда
получим уравнения химического равновесия в безразмерной форме
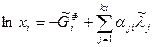 (11)
(11)
Таким образом, в систему уравнений химического равновесия СУХР1 для ТС с произвольным числом химических реакций входят следующие уравнения:
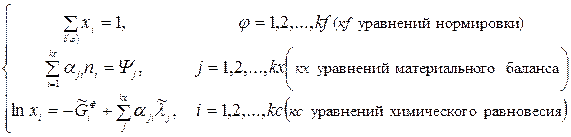 , (12)
, (12)
где 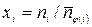 . В СУХР1 (12) неизвестными величинами являются: мольные доли составляющих
. В СУХР1 (12) неизвестными величинами являются: мольные доли составляющих 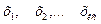 ; количества молей веществ в каждой фазе
; количества молей веществ в каждой фазе 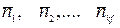 , мольные безразмерные свободные энергии Гиббса атомов
, мольные безразмерные свободные энергии Гиббса атомов 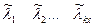 .
.
Таким образом, число неизвестных kc+kf+kx равно числу уравнений (kf+kx+kc) (12).
Рассмотрим пример расчета состава веществ для термодинамической системы с произвольным числом химических реакций. Набор величин 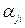 образует матрицу (выделенные цифры) размером кх×кс, причем кх =3, кс =7, а кf =2, как представлено в следующей таблице.
образует матрицу (выделенные цифры) размером кх×кс, причем кх =3, кс =7, а кf =2, как представлено в следующей таблице.
| i(кс) | 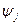
| 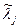
| ||||||||||
| Символ вещества | e- | C | O | CO2+ | СO | C3O2 | C(T) | |||||
| j (кх) | e- | -1 |
= 
| 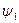
| 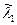
| |||||||
| C | 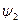
| 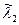
| ||||||||||
| О | 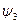
| 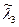
| ||||||||||
| ni | n1 | n2 | n3 | n4 | n5 | n6 | n7 | 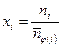
| ||||
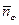
| 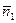
| 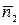
|
Тогда для рассматриваемого примера система уравнений химического равновесия СУХР-1 будет включать уравнения нормировки 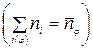 :
:
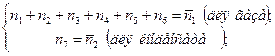
уравнения материального баланса:
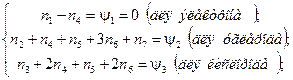
уравнения химического равновесия
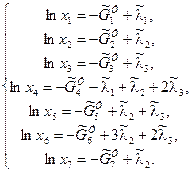
В этой системе уравнений СУХР 1 неизвестными величинами являются: n1, n2, n3, n4, n5, n6, n7; 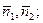
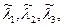 т.е. имеется 12 неизвестных величин и 12 уравнений, входящих в СУХР-1 для данного примера. Если углерод находится в чистой фазе (х 7=1), то ln x 7=0 и
т.е. имеется 12 неизвестных величин и 12 уравнений, входящих в СУХР-1 для данного примера. Если углерод находится в чистой фазе (х 7=1), то ln x 7=0 и 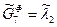 .
.
В СУХР 1 (12) для рассматриваемого примера в качестве химических элементов включается в перечень элементов электрон e- и положительный ион СО 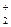 , поскольку в рассматриваемой термодинамической системе происходит реакция ионизации вещества СО2. Положительный ион имеет отрицательный коэффициент
, поскольку в рассматриваемой термодинамической системе происходит реакция ионизации вещества СО2. Положительный ион имеет отрицательный коэффициент 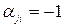 , а электрон – положительный коэффициент
, а электрон – положительный коэффициент 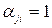 . Для заряженных частиц уравнение материального баланса записывается в той же форме, как и для обычных атомов и называется уравнением квазинейтральности. Так как суммарный заряд термодинамической системы равен нулю, то и материальная постоянная равна нулю -
. Для заряженных частиц уравнение материального баланса записывается в той же форме, как и для обычных атомов и называется уравнением квазинейтральности. Так как суммарный заряд термодинамической системы равен нулю, то и материальная постоянная равна нулю - 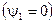 . Уравнения материального баланса получаются почленным перемножением элементов строк матрицы
. Уравнения материального баланса получаются почленным перемножением элементов строк матрицы 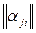 на количества веществ
на количества веществ 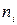 , записанные в предпоследней строке таблицы, где представлены исходные данные и искомые величины для рассмотренного примера.
, записанные в предпоследней строке таблицы, где представлены исходные данные и искомые величины для рассмотренного примера.
 2015-01-21
2015-01-21 489
489








