| № п/п | Схематический чертеж | Формулы и комментарии | |||||||||
z
0 у x | Уравнение плоскости, проходящей через заданную точку М0(x 0, y 0, z 0) – перпендикулярно вектору нормали 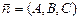 : :
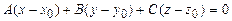
| ||||||||||
z
 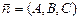
 0 y
х 0 y
х
| Общее уравнение плоскости
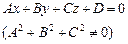
| ||||||||||
z
M2
 M1 M1
M3 0 y x | Уравнение плоскости, проходящей че- рез три точки М1(x 1, y 1, z 1), М2(x 2, y 2, z 2), М3(x 3, y 3, z 3)
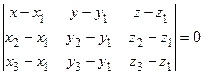
| ||||||||||
| z 0 y x | Уравнение плоскости в отрезках 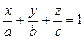 ,
где a, b, c – величины направленных отрезков, отсекаемых плоскостью на координатных осях ,
где a, b, c – величины направленных отрезков, отсекаемых плоскостью на координатных осях
| ||||||||||
| z 0 y x | Угол между двумя плоскостями
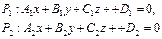
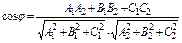
| ||||||||||
| z 0 y x | Условие параллельности двух
плоскостей
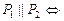 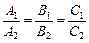
| ||||||||||
| z 0 y x | Условие перпендикулярности двух плоскостей
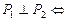 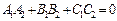
| ||||||||||
      8 8
| z М0 0 y x | Расстояние от точки М0(x0,y0, z0) до плоскости 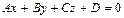
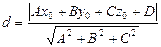
| |||||||||
    9 9
| z
 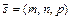
 М0(x0, y0, z0)
0 y
x М0(x0, y0, z0)
0 y
x
| Канонические уравнения прямой в пространстве:
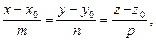 где
где 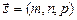 – направляющий вектор прямой – направляющий вектор прямой
| |||||||||
    10 10
| z
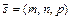

 М0(x0, y0, z0)
y
0
x М0(x0, y0, z0)
y
0
x
| Параметрические уравнения прямой в пространстве:
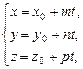 где t – параметр где t – параметр
| |||||||||
                 11 11
| z 0 y x | Общие уравнения прямой в пространстве: 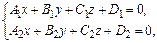
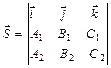
| |||||||||
    12 12
| z
М 2
М 1
0 y x | Уравнения прямой, проходящей через две данные точки
М 1(x 1, y 1, z 1), М 2 (x 2, y 2, z 2)
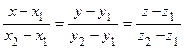
| |||||||||
       13 13
| z
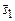 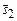
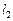 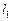 0 y
x
0 y
x
| Угол между двумя прямыми
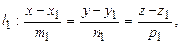
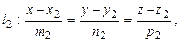
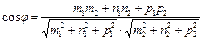
| |||||||||
     14 14
| z
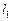
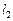 0 y
x
0 y
x
| Условие перпендикулярности двух прямых
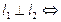 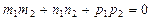
| |||||||||
    15 15
| z
l1
l2
 0 y
x
0 y
x
| Условие параллельности двух прямых
l 1  l 2 l 2 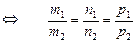
| |||||||||
Таблица производных
| Простая функция | Сложная функция | |
| 1. | 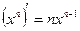 , , 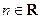
| 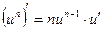 , , 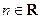
|
| 2. | 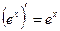
| 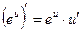
|
| 3. | 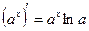
| 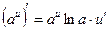
|
| 4. | 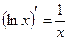
| 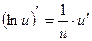
|
| 5. | 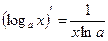
| 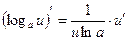
|
| 6. | 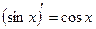
| 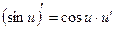
|
| 7. | 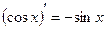
| 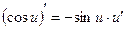
|
| 8. | 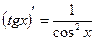
| 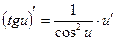
|
| 9. | 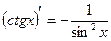
| 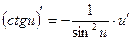
|
| 10. | 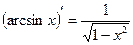
| 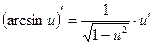
|
| 11. | 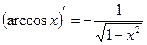
| 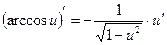
|
| 12. | 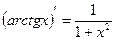
| 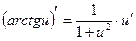
|
| 13. | 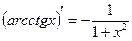
| 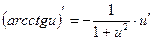
|
 2015-01-21
2015-01-21 352
352











