2014-10-30
920
Рассмотрим на плоскости кривую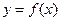 
, являющуюся графиком дифференцируемой функции 
.
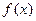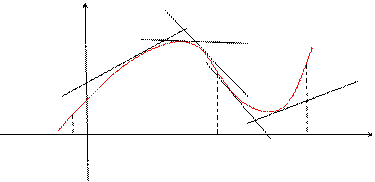
Определение. Мы говорим, что кривая обращена выпуклостью вверх на интервале (а, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Определение. Мы говорим, что кривая обращена выпуклостью вниз на интервале (b, с), если все точки кривой лежат выше любой ее касательной на этом интервале.
Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращенную выпуклостью вниз – вогнутой.
у
а в с x
Рис.1
На рисунке 1 показана кривая, выпуклая на интервале (а, b) и вогнутая на интервале (b, с).
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f (x) отрицательна, т.е.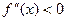 
, то кривая y = f (x) на этом интервале обращена выпуклостью вверх (кривая выпукла).
Теорема 1′. Если во всех точках интервала (b, с) вторая производная функции
f (x) положительна, т.е.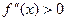 
, то кривая y = f (x) на этом интервале обращена выпуклостью вниз (кривая вогнута).
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба кривой.
|
|
|
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением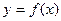 
. Если вторая производная f¢¢ (a) = 0 или f¢¢ (a) не существует и при переходе через точку х = а производная f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
