Определение. Прямая l называется асимптотой кривой, если расстояние от переменной точки M кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Асимптоты функции делятся на два вида:
1) вертикальные асимптоты, т.е. прямые, параллельные оси 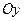 ; они имеют уравнения вида х = а;
; они имеют уравнения вида х = а;
2) наклонные асимптоты, т.е. прямые, не параллельные оси 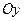 ; они имеют уравнения вида y = kx + b.
; они имеют уравнения вида y = kx + b.
Теорема о вертикальной асимптоте. Прямая х = а является вертикальной асимптотой функции 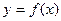 только в том случае, когда
только в том случае, когда 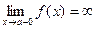 , или
, или 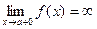 .
.
Теорема о наклонной асимптоте. Прямая 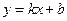 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 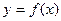 при
при 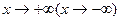 только в том случае, когда существуют (конечные) пределы
только в том случае, когда существуют (конечные) пределы
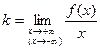 и
и 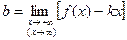 .
.
 2014-10-30
2014-10-30 891
891







