Максимум и минимум функций. Необходимые и достаточные условия существования экстремума

Определение. Точка 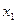называется точкой максимума функции у = f (x), если

cуществует такая 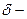окрестность точки 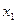_, что для всех 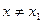из этой окрестности выполняется неравенство f (x) < f ().

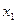Определение. Точка 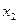называется точкой минимума функции у = f (x),если

cуществует такая 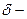окрестность точки 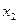_, что для всех 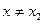из этой окрестности выполняется неравенство f (x)> f ().

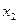Значение функции в точке максимума (минимума) называется максимумом

(минимумом) функции. Максимум (минимумом) функции называется экстремумом функции.

Теорема 1 (необходимое условие существования экстремума). Если дифференцируемая функция у = f (x) имеет экстремум в точке 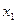, то ее производная в этой точке равна нулю: f¢ (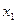) = 0.

Обратное утверждение к этой теореме не верно.

Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Теорема 2 (достаточные условия существования экстремума). Пусть функция f (x) непрерывна в интервале (а, b), который содержит критическую точку 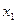, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки 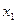). Если при переходе через точку 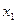слева направо производная функции f¢ (x) меняет знак с плюса на минус, то в точке 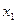функция f (x) имеет максимум, если же производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум, если же производная знака не меняет, то в точке 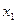экстремума не существует.