Рассмотрим простую зубчатую передачу, состоящую из двух зубчатых колёс внешнего зацепления.
Скорость общей точки Р определим по формуле
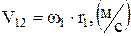 ,
,
где:
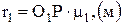 .
.
Из точки Р к прямой 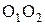 построим отрезок Ра изображающий в масштабе
построим отрезок Ра изображающий в масштабе 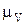 скорость точки Р.
скорость точки Р.
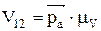
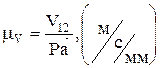
точку а соединим с точкой 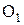 , прямой линией. Продолжив эту линию до пересечения с прямой линией перпендикулярной к
, прямой линией. Продолжив эту линию до пересечения с прямой линией перпендикулярной к 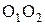 , получим точку С.
, получим точку С.
Прямая ас является планом линейных скоростей 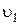 (тэтэ-линией) для точек первого колеса, т.е. геометрическим местом концов векторов скоростей точек этого колеса.
(тэтэ-линией) для точек первого колеса, т.е. геометрическим местом концов векторов скоростей точек этого колеса.
Треугольник 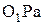 - называется треугольником линейных скоростей для колеса 1.
- называется треугольником линейных скоростей для колеса 1.
Прямая 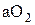 , является планом линейных скоростей
, является планом линейных скоростей 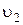 для звена 2 (тэтэ-линией)
для звена 2 (тэтэ-линией)
Определим угловую скорость 1 колеса
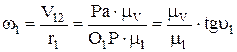 | (2.2) |
Аналогично из треугольника 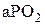 :
:
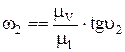
То есть, тангенсы углов наклона тэта-линий треугольников линейных скоростей пропорциональны угловым скоростям соответствующих колёс.
Следовательно, передаточное отношение будет равно:
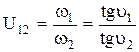
Если тэта-линии, т.е. углы 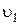 , и
, и 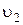 откладываются в одну сторону от линий центров (по часовой стрелке или против неё), то передаточное отношение положительное (колёса вращаются в одну сторону).
откладываются в одну сторону от линий центров (по часовой стрелке или против неё), то передаточное отношение положительное (колёса вращаются в одну сторону).
В противном случае передаточное отношение отрицательное (колёса вращаются в разные стороны).
Построим картину угловых скоростей (рис. 2.18). Перпендикулярно к линии центров проведём прямую линию β-β.
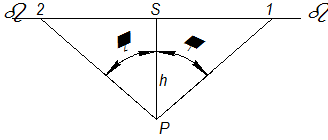 |
| Рис. 2.18 |
Выберем на этой прямой произвольную точку S, проведём через неё параллель к линии центров и отложим вниз от точки S произвольный отрезок 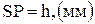 . Из точки Р, как из полюса, проведём лучи, параллельные тэта-линиям 1 и 2. Эти лучи пересекут прямую β-β в точках 1 и 2. Рассмотрим треугольник
. Из точки Р, как из полюса, проведём лучи, параллельные тэта-линиям 1 и 2. Эти лучи пересекут прямую β-β в точках 1 и 2. Рассмотрим треугольник 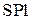 :
:
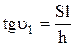
Подставив эту формулу в зависимость (2.40) получим:
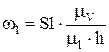
Обозначив
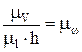 ,
,
получим
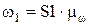
аналогично, 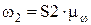 ,тогда передаточное отношение:
,тогда передаточное отношение:
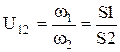
Таким образом, передаточное отношение - это отношение отрезков на картине угловых скоростей (или чисел оборотов в минуту). Допустим, что построенная картина выполнена в масштабе 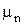 , т.е. является картиной чисел оборотов в минуту, так как
, т.е. является картиной чисел оборотов в минуту, так как 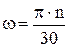 , следовательно:
, следовательно:

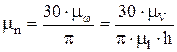
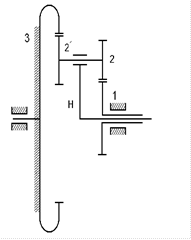
Рассмотрим кинематическое исследование на примере планетарного механизма (рис. 2.19).
Определим скорость 1 колеса:
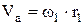
Выбрав масштаб 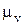 , откладываем отрезок
, откладываем отрезок 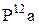 . Если соединить точку а с точкой А, то получим тэта-линию колеса 1. Точка
. Если соединить точку а с точкой А, то получим тэта-линию колеса 1. Точка 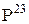 третьего колеса неподвижна, т.е.
третьего колеса неподвижна, т.е. 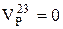 . Следовательно, и сателлит 2 в этой точке имеет скорость равную нулю. Таким образом, положение тэта-линии сателлита 2 определяется двумя точками а и
. Следовательно, и сателлит 2 в этой точке имеет скорость равную нулю. Таким образом, положение тэта-линии сателлита 2 определяется двумя точками а и 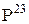 . Точка В принадлежит и сателлиту и водилу, поэтому линейную скорость получим, спроектировав точку В на тэта-линию 2. Соединив, точки А и В получим тэта-линии водила Н.
. Точка В принадлежит и сателлиту и водилу, поэтому линейную скорость получим, спроектировав точку В на тэта-линию 2. Соединив, точки А и В получим тэта-линии водила Н.
 |
| Рис. 2.19 |
2.5. Синтез планетарных механизмов
Синтез планетарных механизмов - это определение числа зубьев колёс механизма, исходя из заданного передаточного отношения.
Подбор чисел зубьев должен быть произведён так, чтобы удовлетворялись условия соосности, соседства и сборки.
 |  |
| а) | б) |
| Рис. 2.20 |
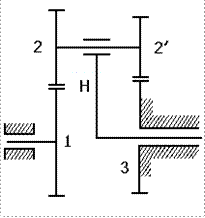
Условие соосности заключается в том, чтобы геометрические оси ведущего и ведомого валов совпадали. Для механизма образованного двумя внешними зацеплениями (рис. 2.20 а) межосевое расстояние определяется по формуле:
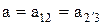
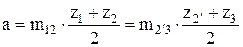
где 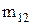 и
и 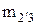 модули зубчатых зацеплений пар колес 12 и 2'3 соответственно.
модули зубчатых зацеплений пар колес 12 и 2'3 соответственно.
Обозначим: 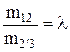 .
.
Получим уравнения соосности:
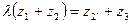 .
.
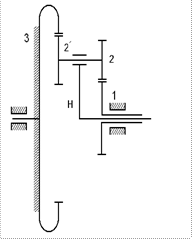
Для механизма образованного двумя парами зубчатых колёс, одна- с внешним, а другая - с внутренним зацеплением (рис. 20 б) межосевое расстояние:
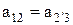 ,
,
то есть: 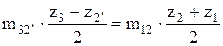
Следовательно, условие соосности для этого случая:
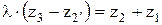 .
.
Условие соседства заключается в том, чтобы окружности вершин сателлитов (рис. 2.21) не касались и не пересекались, то есть 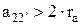 ,
, 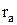 - радиус выступов сателлита.
- радиус выступов сателлита.
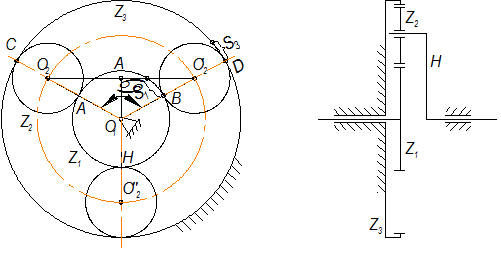 |
| Рис. 2.21 |
Межосевое расстояние между сателлитами, не входящими в зацепление между собой:
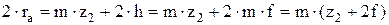
где, f-коэффициент высоты головки зуба. f=1
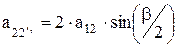
где: 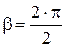 ;
;
k-число сателлитов
После подстановки выражения межосевого расстояния пары зубчатых колёс 1 и 2
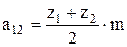 , получим
, получим
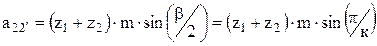
Следовательно, условие соседства можно записать:
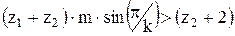
Условие сборки требует, чтобы зубья каждого сателлита вошли в зацепление с обоими центральными колёсами. Для планетарных механизмов условие сборки определяется по формулам, соответствующим типу механизма (рис. 22):
 |  | 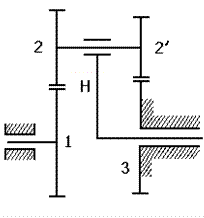 |
| а) | б) | в) |
| Рис. 2.22 |
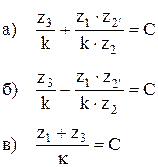
 2015-01-22
2015-01-22 2068
2068
