Арбитражная теория Росса (arbitrage theory - ART) утверждает, что доходность акции зависит частично от макроэкономических факторов и частично от факторов, влияющих на специфический (диверсифицируемый) риск. Равновесная модель САРМ объясняет различие ожидаемых доходностей акций ki. различной чувствительностью к доходности рыночного портфеля, т.е. различием β-коэффициентов. Арбитражная теория Росса также ставит цель объяснить различие ожидаемых доходностей по акциям в ситуации равновесия. Отличие от САРМ заключается в предположении о связи доходности с некоторым количеством факторов. Доходность рыночного портфеля (как в САРМ) может быть одним из факторов.
Арбитражная теория — это альтернатива САРМ, где доходность акции является линейной функцией одного общего фактора — доходности рыночного портфеля. Идея компенсации большего риска по сравнению с безрисковыми активами остается неизменной. Если есть безрисковый вариант займа и инвестирования (этот вариант обеспечивает доходность или стоимость капитала при займе денег в размере kf), то: 1) за больший риск инвесторы требуют большую доходность; 2) получение повышенной доходности означает наличие факторов риска. Инвесторы на рынке стремятся увеличить доходность портфелей без увеличения риска. Такая возможность может быть реализована через арбитражный портфель, т.е. формирование портфеля путем одновременной продажи акций по относительно высокой цене и покупки этих же акций в другом месте по относительно низкой цене. Такая операция позволит инвестору, не вкладывая средства, получить безрисковый доход.
Арбитражные возможности появляются, если по акциям или портфелям с одинаковой чувствительностью к факторам ожидается различная доходность. Инвесторы устремляются к получению безрискового дохода, и возможность арбитража исчерпывается. Таким образом, в равновесии акции и портфели с одинаковой чувствительностью к факторам имеют одинаковые значения ожидаемой доходности (с поправкой на специфический риск).
Преимуществом АРМ является меньшее число предположений о поведении инвестора на рынке по сравнению с САРМ. Кроме того, существуют многопериодные модификации АРМ, в то время как САРМ однопериодная модель.
Предполагается, что фактическая (наблюдаемая) доходность любой акции i является линейной функцией z факторов:
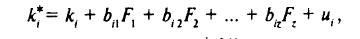
где ki* — наблюдаемая доходность по акции i; %!
ki — ожидаемая доходность акции i;
biz — чувствительность доходности акции i к фактору z (иногда используется термин "факторная нагрузка");
F z — значение фактора z,
u i— случайная величина (с нулевым средним значением), как компонента несистематического риска по акции i.
В модели рассматриваются портфели из имеющихся на рынке акций и выводится условие существования арбитражных портфелей. Предполагается, что число включенных в рассмотрение акций значительно превышает число факторов z. Построение арбитражного портфеля означает отсутствие дополнительного инвестирования (деньги для покупки ценных бумаг образуются через продажу других ценных бумаг) и отсутствие риска. Например, пусть индивид имеет портфель акций и хочет заработать на арбитражных операциях. Инвестор не предполагает инвестировать в изменение долей акций в имеющемся портфеле. Изменение портфеля достигается изменением стоимости акции i в портфеле. Это изменение обозначим через wi. wi показывает вес акции i в арбитражном портфеле. Нулевое инвестирование означает, что Σwi = 0. Безрисковость портфеля требует отсутствия систематического и несистематического риска.
Доходность портфеля из п акций равна взвешенной сумме доходности по отдельным акциям, включенным в портфель:
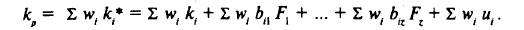
Элиминирование систематического риска достигается через подбор wi таким образом, чтобы для каждого фактора z взвешенная сумма мультипликаторов bz была равна нулю (мультипликаторы систематического риска по каждому фактору дают средневзвешенное нулевое значение): Σwibiz = 0 по каждому фактору от 1 до z. Чувствительность портфеля к фактору z равна средневзвешенной чувствительностей акций, включенных в портфель.
Рассмотрение большого числа активов в портфеле позволяет устранить специфический риск и при большом значении п взвешенная сумма ui →0. Σwiui = 0
Таким образом, диверсификация портфеля позволяет записать выражение для доходности портфеля без последнего слагаемого специфического риска. Итоговое выражение доходности портфеля:
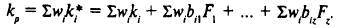
Фактически построен портфель с нулевым бета по каждому фактору, для него не требуется дополнительных инвестиций (какие-то значения wi положительны, что означает покупку акций, какие-то — отрицательны, что означает продажу). Систематический риск устранен. Если доходность kp положительна, то портфель является арбитражным и инвестор будет стремиться построить его. Покупка и продажа определенных акций на рынке большим числом инвесторов приведут к изменению цен и повлияют на ожидаемую доходность. Доходность портфеля не может быть случайной величиной: kp = Σ wiki
В ситуации равновесия доходность построенного портфеля (и всех других арбитражных портфелей) должна быть нулевой: Σ wiki = 0
Тогда из линейной алгебры следует, что вектор ожидаемой доходности ki может быть представлен как линейная комбинация вектора постоянных значений (коэффициентов λ.) и вектора мультипликаторов. Должно существовать z + 1 постоянных коэффициентов λ0, λ1, λ2,..., λz, таких, которые позволят разложить ожидаемую доходность акции i:
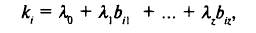
где biz — чувствительность доходности акции i к фактору z.
Для интерпретации коэффициентов λ рассмотрим безрисковый актив с доходностью kf. kf — постоянная величина, и чувствительность к факторам у нее нулевая boz = 0 для всех z = 1,... Следовательно, kf = λ0. Теперь выражение для ki можно представить в виде премии к безрисковому активу:
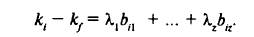
В этом случае получаем экономический смысл для коэффициентов λz — это премия за риск (цена риска) в равновесии для фактора z.
Так как построена линейная зависимость, то естественно представить ее в виде стандартного выражения прямой: у = а + b х, где b равен тангенсу угла наклона прямой.
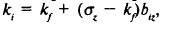
где σz — ожидаемая доходность портфеля с единичной чувствительностью к фактору z и нулевой чувствительностью к другим факторам. Такой портфель носит название чистого факторного портфеля. Тогда выражение цены риска принимает вид
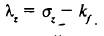 .
.
Коэффициент λ показывает избыточную доходность (по сравнению с безрисковой доходностью) по чистому факторному портфелю. Это премия за факторный риск.
Часто для представления арбитражной модели используется версия с премиями за факторный риск:
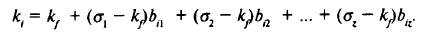
Некоторые акции более чувствительны к конкретному фактору, чем другие. Например, акции РАО "Газпром" более чувствительны к изменению цен на бензин, чем акции кондитерской фабрики "Красный Октябрь". Если фактор 1 — изменение цен на бензин, то 6, будет выше для РАО "Газпром", чем для АО "Красный Октябрь".
Арбитражная модель не определяет конкретное число факторов и их значимость для данной акции, так как для каждой акции значимыми будут свои факторы. Факторами могут быть фондовый индекс (как в САРМ рыночный портфель), валовой национальный продукт, цены на энергоносители, процентная ставка и др. Ряд исследований выявил наиболее значимые факторы. Например, расчеты по американскому рынку выявили в числе значимых макроэкономических факторов такие, как изменения в отраслевом производстве, инфляция, индивидуальное потребление, предложение денег и процентная ставка. Агентство Salomon Brothers при оценках по многофакторной модели включает в рассмотрение пять факторов: инфляцию, темп роста валового национального продукта (ВНП), процентную ставку, индекс изменения цен на нефть, темп роста расходов на оборону.
Обобщенно можно выделить три группы факторов, обязательно включаемых в арбитражную модель:
1) показатели общей экономической активности (это может быть темп роста промышленного производства, темп роста усредненных продаж, темп роста ВНП);
2) показатели, отражающие инфляцию;
3) показатели процентной ставки (разница между долгосрочной и краткосрочной ставками, ставка доходности фондового (рыночного) индекса).
?Может ли количество факторов, определяющих доходность актива, изменяться со временем? Что может породить эти изменения?
 2015-01-30
2015-01-30 1608
1608








