2015-01-30
840
Ранее получены формулы для определения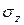 
от 
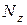и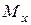 
: 
, 
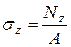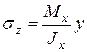. По аналогии можно записать формулу для 
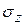от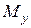 
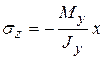(а). В этих формулах х и у координаты точки сечения бруса, где определяется 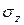. Очевидно, что при 
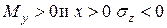(сжатие) получается. Поэтому в формуле (а) стоит знак минус. При одновременном действие в сечении бруса 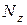, 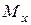и 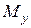суммарные напряжения в любой точки сечения с координатами х и у можно определить так
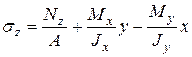(7.2)
Это одна из основных формул сопротивления материалов. В (7.2) 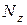, , 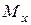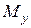и координаты точки сечения х и у надо подставлять со своими знаками. Если 
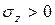получится, значит в этой точке сечения – растяжение, если 
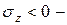то сжатие. Это важно при оценке прочности хрупких материалов.
От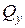 
в сечении бруса возникают 
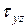, определяемые по известной формуле Журавского 
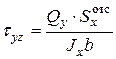. Аналогично, от 
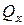возникают 
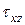, определяемые по формуле 
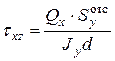. От кручения 
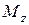круглых валов возникают 
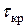, определяемые известной формулой 
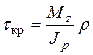. Направления касательных напряжений от 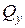, 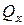и 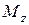были выяснены раньше. В каждой точки сечения эти напряжения надо суммировать геометрически (векторно), т.е. суммарные напряжения
 |
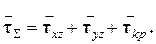
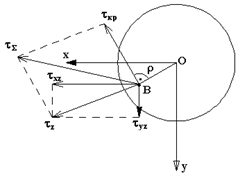Рис.7.4
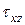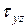, и 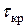в т. В круглого сечения бруса. Определив в этой же точке «В» 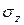от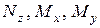 
по (7.2), можно оценить прочность в точке «В» сечения по одной из теорий прочности. Например, по III теории прочности получим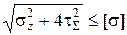 
Рассмотрим подробнее частные случаи сложного сопротивления бруса.
