 |
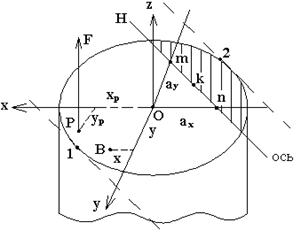
Рис.7.9
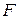 , приложенных в т. «Р» (полюс) не совпадающей с т. О – центром тяжести сечении (рис. 7.9). При переносе силы
, приложенных в т. «Р» (полюс) не совпадающей с т. О – центром тяжести сечении (рис. 7.9). При переносе силы 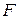 в т. О брус нагрузится продольной силой
в т. О брус нагрузится продольной силой 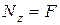 и изгибающим моментом
и изгибающим моментом 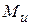 , причем все сечения бруса по его длине будут загружены одинаково.
, причем все сечения бруса по его длине будут загружены одинаково. Определение напряжений
Пусть на брус в т. «Р» с координатами 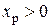 и
и 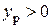 действует растягивающая сила
действует растягивающая сила 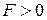 (рис. 7.9). Перенесем силу
(рис. 7.9). Перенесем силу 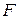 сначала на ось
сначала на ось 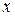 (плечо
(плечо 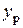 ), а затем в т. О (плечо
), а затем в т. О (плечо 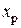 ). В итоге в поперечном сечении бруса возникнут:
). В итоге в поперечном сечении бруса возникнут:
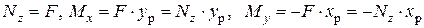 (6)
(6)
В произвольной точке «В» сечения с координатами 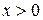 и
и 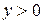
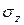 найдем по (7.2)
найдем по (7.2)
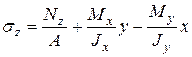 (7)
(7)
Подставляя (6) в (7) получим
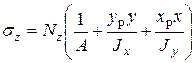 (7.9)
(7.9)
Учитывая, что 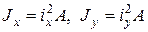 и подставляя в (7.9)
и подставляя в (7.9)
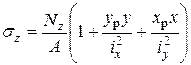 (7.10)
(7.10)
В произвольных случаях нагружения в формулы (7.9) и (7.10) 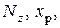
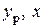 и
и 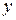 надо подставлять со своими знаками в заданных главных центральных осях
надо подставлять со своими знаками в заданных главных центральных осях 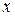 и
и 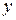 .
. 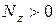 при растяжении бруса,
при растяжении бруса, 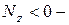 при сжатии.
при сжатии.
Эпюры 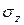 в сечении строятся аналогично как при косом изгибе.
в сечении строятся аналогично как при косом изгибе.
Нейтральная ось (Н.О)
Обозначим координаты точек на Н.О через 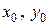 . В этих точках
. В этих точках 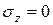 . Подставляя
. Подставляя 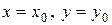 и
и 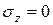 в (7.10) и сокращая на
в (7.10) и сокращая на 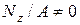 получим
получим
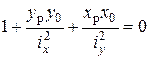 (7.11)
(7.11)
Это уравнение Н.О. Видно, что это уравнение прямой (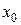 и
и 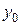 в первой степени), не проходящей через начало координат (т.к. при
в первой степени), не проходящей через начало координат (т.к. при 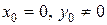 ). Положение Н.О удобно определять отрезками
). Положение Н.О удобно определять отрезками 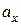 и
и 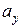 , которые Н.О отсекает на осях координат (рис. 7.9) и проходит через т. «
, которые Н.О отсекает на осях координат (рис. 7.9) и проходит через т. «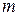 » и т. «
» и т. «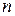 ». Допустим пока, что
». Допустим пока, что 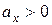 и
и 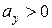 . Точка «
. Точка «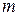 » в этом случае имеет координаты
» в этом случае имеет координаты 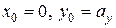 . Подставляем это в (7.11) получим
. Подставляем это в (7.11) получим
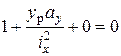
Отсюда
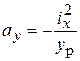 (7.12а)
(7.12а)
Аналогично т. «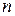 ». Подставляя
». Подставляя 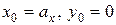 найдем
найдем
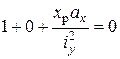
Отсюда
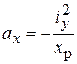 (7.12в)
(7.12в)
Из (7.12) видно, что при 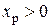 и
и 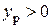 получим
получим 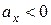 и
и 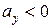 , т.е. наше допущение неверно и правильно Н.О показана на рис. 7.9.
, т.е. наше допущение неверно и правильно Н.О показана на рис. 7.9.
Свойства нейтральной оси
Из формул (7.12) следует:
1. Положение Н.О не зависит от величины и знака 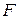 .
.
2. Н.О и полюс т. «Р» лежат по разные стороны от центра тяжести сечения т. О.
3. При удалении полюса от т. О, Н.О приближается к нему и наоборот.
4. Если полюс расположен на одной из осей координат, то Н.О перпендикулярна к этой оси (при  полюс на оси
полюс на оси 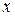 ,
, 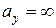 , т.е. Н.О параллельна оси
, т.е. Н.О параллельна оси 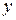 или перпендикулярна оси
или перпендикулярна оси 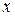 ).
).
5. При вращении Н.О вокруг произвольной точки «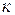 » на ней (рис. 7.9), полюс перемещается по прямой линии, не проходящей через т. О. Подставим в (7.11)
» на ней (рис. 7.9), полюс перемещается по прямой линии, не проходящей через т. О. Подставим в (7.11) 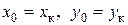 . Получим уравнение, которое относительно координат
. Получим уравнение, которое относительно координат 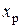 и
и 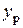 есть уравнение прямой не проходящей через т. О.
есть уравнение прямой не проходящей через т. О.
6. Н.О делит сечение на две зоны: растянутую и сжатую, заштрихованную на рис. 7.9 при 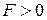 .
.
Из соотношений (7.12) можно решить обратную задачу: зная положение Н.О (т.е. 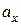 и
и 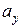 ) найти положение полюса, т.е.
) найти положение полюса, т.е. 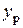 и
и 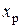
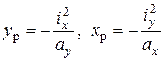 (7.13)
(7.13)
Определив положение Н.О, проведем к контуру сечения касательные, параллельные Н.О. Получим т.1 с координатами 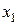 и
и 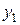 и т.2 с координатами
и т.2 с координатами 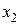 и
и 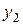 . Если в т. «Р» действует
. Если в т. «Р» действует 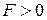 , то в т. 1 будут
, то в т. 1 будут 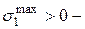 растягивающие (р), а в т. 2
растягивающие (р), а в т. 2 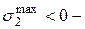 сжимающие (сж). Обычно колонны изготавливают из хрупких материалов, поэтому прочность проверяется отдельно в растянутой и сжатой зонах по формулам (7.9) или (7.10):
сжимающие (сж). Обычно колонны изготавливают из хрупких материалов, поэтому прочность проверяется отдельно в растянутой и сжатой зонах по формулам (7.9) или (7.10):
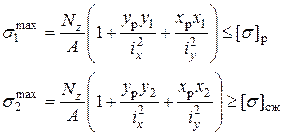 (8)
(8)
При действии на колонну сжимающей силы 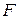 в т. 1 будут
в т. 1 будут 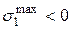 , в т. 2
, в т. 2 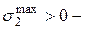 растягивающие.
растягивающие.
Размеры сечения обычно определяются методом подбора: задают размеры, определяют положение Н.О, т.1 и т.2 и проверяют в них прочность по (8). Если эти условия не выполняются, меняют размеры сечения и снова проверяют.
Для брусьев с сечениями типа прямоугольника, двутавра или швеллера из пластичных материалов, у которых 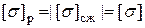 , первую попытку можно провести как при косом изгибе по второй формуле (7.8), определив
, первую попытку можно провести как при косом изгибе по второй формуле (7.8), определив 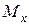 и
и 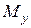 по (6), а
по (6), а 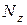 пока не учитывать. Здесь подбор размеров сечения проводить так, как указано ниже формулы (7.8). Определив размеры сечения, делать проверку по (8) с учетом
пока не учитывать. Здесь подбор размеров сечения проводить так, как указано ниже формулы (7.8). Определив размеры сечения, делать проверку по (8) с учетом 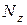 .
.
Ядро сечения
Для колонн из хрупких материалов (чугун, бетон, камень и т.д.), плохо работающих на растяжение желательно, чтобы от сжимающей силы 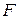 во всех точках сечения были только сжимающие напряжения. Этого можно добиться, если Н.О не пересекает сечение колонны, а согласно свойства 3 Н.О. это получим, ограничивая удаление полюса «Р» от т. О.
во всех точках сечения были только сжимающие напряжения. Этого можно добиться, если Н.О не пересекает сечение колонны, а согласно свойства 3 Н.О. это получим, ограничивая удаление полюса «Р» от т. О.
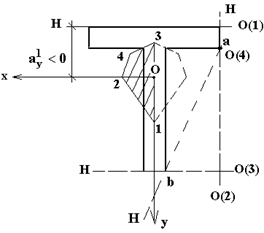 Рис.7.10 | Ядро сечения – это некоторая область вокруг ц.т. (т. О) сечения, внутри которой можно располагать полюс т. «Р», не вызывая в сечении колонны напряжений разных знаков (только знака 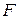 ). Если полюс «Р» расположен на границе ядра сечения, то Н.О только касается контура сечения. На этом и основан порядок построения ядра сечения, показанный на рис. 7.10: ). Если полюс «Р» расположен на границе ядра сечения, то Н.О только касается контура сечения. На этом и основан порядок построения ядра сечения, показанный на рис. 7.10: |
1. Даем Н.О все возможные положения, касательные к контуру сечения, учитывая симметрию сечения. Это Н.О (1) ¸ Н.О (4).
2. Для каждого положения Н.О (1) ¸ Н.О (3), т.е. вертикальных и горизонтальных, легко определить величины и знаки отрезков 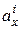 и
и 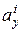 (
(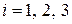 ), зная размеры сечения и положение главных центральных осей
), зная размеры сечения и положение главных центральных осей 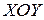 .
.
Например, для Н.О (1) 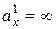 (Н.О (1) и ось
(Н.О (1) и ось 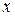 параллельны),
параллельны), 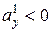 показан на рис. 7.10.
показан на рис. 7.10.
3. По формулам (7.13) вычисляем для каждого положения Н.О координаты полюса, т.е. 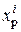 и
и 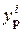 и определяем эти т.1 ¸ т.3 на рисунке сечения, выполненного в масштабе (рис. 7.10).
и определяем эти т.1 ¸ т.3 на рисунке сечения, выполненного в масштабе (рис. 7.10).
Для Н.О (4) – наклонной, определить 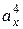 и
и 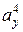 затруднительно. Поэтому здесь лучше использовать уравнение Н.О в виде (7.11). Н.О (4) проходит через т.т. «а» и «b» сечения, координаты которых
затруднительно. Поэтому здесь лучше использовать уравнение Н.О в виде (7.11). Н.О (4) проходит через т.т. «а» и «b» сечения, координаты которых 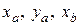 и
и 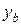 легко определить (величины и знаки). Подставляем их в (7.11) вместо
легко определить (величины и знаки). Подставляем их в (7.11) вместо 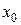 и
и 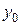 получим
получим
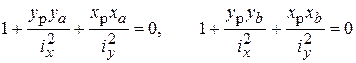 (9)
(9)
Решаем эти два уравнения для вычисления 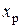 и
и 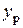 , это и будут координаты т. 4 на ядре. Из рис. 7.10 видно, что Н.О из одного положения в другое переводятся вращением вокруг точек сечения колонны, а согласно свойства 5 Н.О полюс при этом перемещается по прямой. Поэтому т.1 ¸ т.4 на рис. 7.10 надо соединить прямыми линиями. Получим половину ядра сечения, заштрихованную на рис. 7.10. Сечение колонны симметрично относительно оси
, это и будут координаты т. 4 на ядре. Из рис. 7.10 видно, что Н.О из одного положения в другое переводятся вращением вокруг точек сечения колонны, а согласно свойства 5 Н.О полюс при этом перемещается по прямой. Поэтому т.1 ¸ т.4 на рис. 7.10 надо соединить прямыми линиями. Получим половину ядра сечения, заштрихованную на рис. 7.10. Сечение колонны симметрично относительно оси 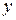 , поэтому и ядро его сечения симметрично относительно оси
, поэтому и ядро его сечения симметрично относительно оси 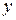 (вторая половина ядра показана пунктиром).
(вторая половина ядра показана пунктиром).
Ядра сечений некоторых фигур
1. Прямоугольное сечение 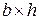 :
:
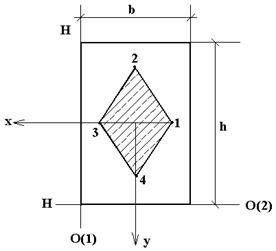 Рис.7.11 Рис.7.11 | Ввиду двух осей симметрии 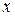 и и 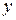 достаточно двух положений Н.О Н.О (1): достаточно двух положений Н.О Н.О (1): 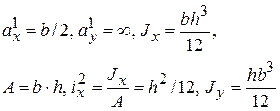 , , 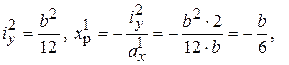 , , |
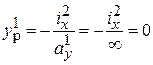 т.е. т.1 на оси
т.е. т.1 на оси 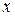 . Н.О (2):
. Н.О (2): 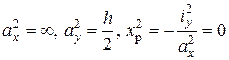 , т.е. т.2 на оси
, т.е. т.2 на оси 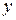 .
. 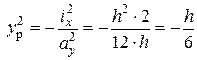 . Строим т.2., т.3 симметрична т.1, а т.4 симметрична т.2. Соединяем т.1¸т.4 прямыми линиями, получим ядро сечения в виде ромба с размерами
. Строим т.2., т.3 симметрична т.1, а т.4 симметрична т.2. Соединяем т.1¸т.4 прямыми линиями, получим ядро сечения в виде ромба с размерами 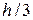 и
и 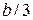 .
.
2. Круглое сечение радиуса 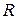 .
.
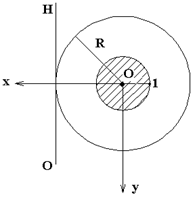 Рис.7.12 Рис.7.12 | Ввиду осевой симметрии, достаточно одного положения Н.О 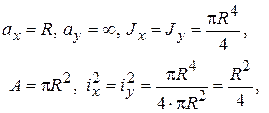 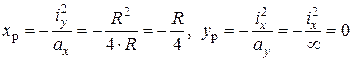 . Получим т.1 на ядре. Ядро сечения здесь круг с радиусом . Получим т.1 на ядре. Ядро сечения здесь круг с радиусом 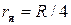 . . |
 2015-01-30
2015-01-30 1328
1328