Здесь в поперечных сечениях бруса могут быть 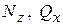 ,
, 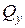 ,
, 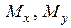 , а
, а 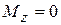 . Косой изгиб может быть чистым, когда вдоль бруса отсутствуют
. Косой изгиб может быть чистым, когда вдоль бруса отсутствуют 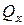 =
= 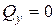 и поперечным, когда
и поперечным, когда 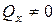 и
и 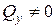 , а
, а 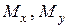 переменны по длине бруса. Косой изгиб может быть плоским, когда вся внешняя нагрузка лежит в одной плоскости и не плоским, когда нагрузки в плоскостях
переменны по длине бруса. Косой изгиб может быть плоским, когда вся внешняя нагрузка лежит в одной плоскости и не плоским, когда нагрузки в плоскостях 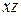 и
и 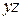 изменяются произвольно по длине бруса.
изменяются произвольно по длине бруса.
Величины и знаки 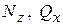 ,
, 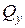 ,
, 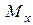 и
и 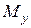 в любом сечении бруса определяются из эпюр. Введем понятие полный изгибающий момент, определяемый так
в любом сечении бруса определяются из эпюр. Введем понятие полный изгибающий момент, определяемый так
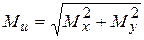 (7.3)
(7.3)
Если 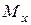 и
и 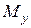 представить в виде векторов (длина векторов определяет величину
представить в виде векторов (длина векторов определяет величину 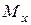 и
и 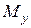 , а направления по правилу правого «буравчика»), то
, а направления по правилу правого «буравчика»), то 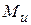 есть геометрическая сумма
есть геометрическая сумма 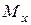 и
и 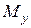 , что показано на рис. 7.5. Положение
, что показано на рис. 7.5. Положение 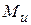 удобно определять углом
удобно определять углом 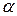 , который он составляет с осью
, который он составляет с осью 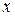 (
(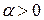 отсчитывается от оси
отсчитывается от оси 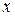 против хода часовой стрелки). Из рис. 7.5 видно:
против хода часовой стрелки). Из рис. 7.5 видно:
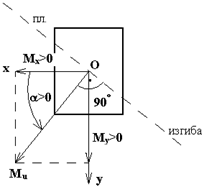 Рис.7.5 Рис.7.5 |  (1) Отсюда (1) Отсюда  (2) Нормальное напряжение (2) Нормальное напряжение  в любой точки сечения с координатами в любой точки сечения с координатами 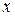 и и 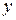 определяется по формуле (7.2), полагая в ней определяется по формуле (7.2), полагая в ней 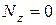 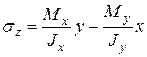 (7.4) (7.4) |
С учетом (1) 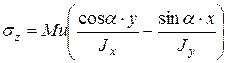 (7.5)
(7.5)
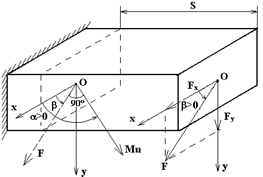 Рис.7.6 Рис.7.6 | В формулы (7.4) и (7.5) все надо подставить со своими знаками: знаки 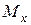 и и 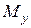 берутся из эпюр, берутся из эпюр, 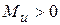 всегда. Величина и знак всегда. Величина и знак 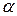 определяется из формулы (2). Во многих случаях известны величина и направле-ние поперечной нагрузки ( определяется из формулы (2). Во многих случаях известны величина и направле-ние поперечной нагрузки (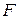 или или 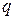 ), направлениях их будем определять углом ), направлениях их будем определять углом 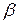 , отсчи-тываемый от оси , отсчи-тываемый от оси 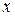 (рис. 7.6), (рис. 7.6), |
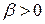 против хода часовой стрелки. В произвольном сечении балки на расстоянии
против хода часовой стрелки. В произвольном сечении балки на расстоянии 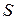 от торца от
от торца от 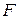 возникнет
возникнет 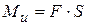 , который с направлением
, который с направлением 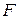 составляет угол 90°, а с осью
составляет угол 90°, а с осью 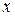 угол
угол 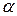 , т.е.
, т.е. 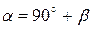 . Зная
. Зная 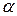 и
и 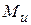 ,
, 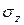 можно вычислять по (7.5). Но проще силу
можно вычислять по (7.5). Но проще силу 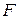 разложить по осям
разложить по осям 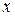 и
и 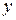 , т.е.
, т.е. 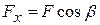 ,
, 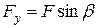 (видно из рис. 7.6). От
(видно из рис. 7.6). От 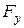 строят эпюру
строят эпюру 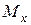 , а от
, а от 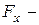 эпюру
эпюру 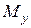 и далее
и далее 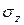 определяют по формуле (7.4). Аналогично и от погонной нагрузки
определяют по формуле (7.4). Аналогично и от погонной нагрузки 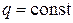 :
: 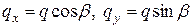 , от
, от 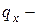 эпюру
эпюру 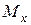 , от
, от 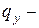 эпюру
эпюру 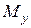 .
.
Нейтральная ось (Н.О)
Нейтральная ось – линия в сечении балки, относительно которой сечение поворачивается, оставаясь плоским (гипотеза Бернулли). Обозначим координаты точек на нейтральной оси через 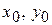 . Согласно определения Н.О в этих точках
. Согласно определения Н.О в этих точках 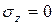 . Подставляя
. Подставляя 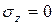 ,
, 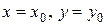 в (7.5), сокращая на
в (7.5), сокращая на 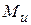 получим
получим
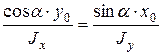 (3)
(3)
Это уравнение Н.О. Видно, что это уравнение прямой линии проходящей через начало координат, т.к. при 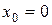 должно быть
должно быть 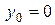 . Положение Н.О удобно определять через угол ее наклона к одной из осей координат. Обозначим
. Положение Н.О удобно определять через угол ее наклона к одной из осей координат. Обозначим 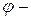 угол наклона Н.О к оси
угол наклона Н.О к оси 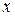 (рис. 7.7),
(рис. 7.7), 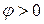 против хода часовой стрелки.
против хода часовой стрелки.
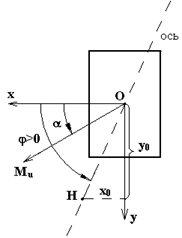 Рис.7.7 Рис.7.7 | Из рис. 7.7 видно 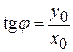 (4) Из (3) следует (4) Из (3) следует 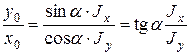 (5) С учетом (4) получим (5) С учетом (4) получим 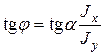 (7.6) Плоскость изгибающей нагрузки перпендику-лярна (7.6) Плоскость изгибающей нагрузки перпендику-лярна 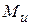 , а плоскость изгиба (прогибов) пер- , а плоскость изгиба (прогибов) пер- |
пендикулярна Н.О. При 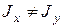 эти плоскости не совпадают
эти плоскости не совпадают 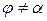 , поэтому эту деформацию и назвали «косой изгиб». При
, поэтому эту деформацию и назвали «косой изгиб». При 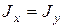 (сечение квадратное, круглое и т.д.)
(сечение квадратное, круглое и т.д.) 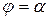 и косого изгиба не будет.
и косого изгиба не будет.
Определение напряжений. Расчеты на прочность.
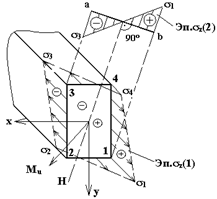 |
Рис.7.8
 в аксонометрии (Эп.
в аксонометрии (Эп.  ) или в плоскости сечения (Эп.
) или в плоскости сечения (Эп. 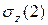 ), используя формулы (7.4) или (7.5), эпюры показаны на рис. 7.8. Для построения эпюр
), используя формулы (7.4) или (7.5), эпюры показаны на рис. 7.8. Для построения эпюр 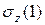 вычисляют
вычисляют 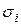 в угловых точках сечения (
в угловых точках сечения (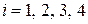 ) и откладывают их в масштабе с учетом знаков (
) и откладывают их в масштабе с учетом знаков ( – растяжение, наружу от сечения, (–) – сжатие - противоположно).
– растяжение, наружу от сечения, (–) – сжатие - противоположно). 
Далее точки соединяют прямыми линиями, т.к. из (7.4) и (7.5) видно, что 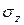 линейны по координатам
линейны по координатам 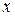 и
и 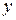 . Итак, Н.О делит сечение на две зоны, растянутую
. Итак, Н.О делит сечение на две зоны, растянутую  и сжатую (–) (рис. 7.8).
и сжатую (–) (рис. 7.8).
Для построение эпюры 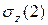 перпендикулярно Н.О проводят линию
перпендикулярно Н.О проводят линию 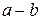 . В т. «
. В т. «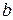 » в масштабе откладывают
» в масштабе откладывают 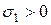 , а в т. «а»
, а в т. «а» 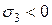 и далее соединяют их прямой линией.
и далее соединяют их прямой линией.
Из эпюр 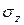 видно, что экстремальные напряжения возникают в точках сечения, наиболее удаленных от Н.О. Это будут т.1 и т.3. В них
видно, что экстремальные напряжения возникают в точках сечения, наиболее удаленных от Н.О. Это будут т.1 и т.3. В них 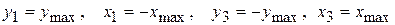 и по (7.4)
и по (7.4)
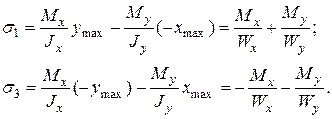 где
где 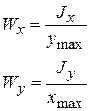
Итак, в т.1 и т.3 сечения 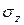 равны по величине и противоположны по знаку
равны по величине и противоположны по знаку
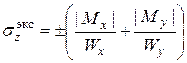 (7.7)
(7.7)
Здесь знак выбирают по физическому смыслу,  в растянутой зоне, (–) в сжатой. Аналогично определяются
в растянутой зоне, (–) в сжатой. Аналогично определяются 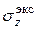 в других сечения с выступающими углами.
в других сечения с выступающими углами.
Для балок из пластичных материалов, одинаково работающих на растяжение и сжатие, условие прочности в опасном сечении бруса можно записать так с учетом (7.7)
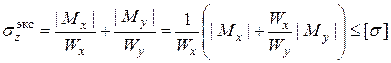 (7.8)
(7.8)
При подборе размеров сечения балки используем вторую формулу (7.8), при этом надо задать отношение 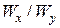 с учетом рационального расположения сечения: для прямоугольника при
с учетом рационального расположения сечения: для прямоугольника при 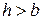 (размер
(размер 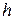 вдоль оси
вдоль оси 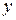 ) если
) если 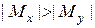 то
то 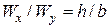 ; если
; если 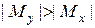 , то размер
, то размер 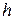 вдоль оси
вдоль оси 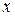 (т.е. повернуть на 90°) и
(т.е. повернуть на 90°) и 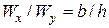 . Условие прочности одно, а неизвестных два
. Условие прочности одно, а неизвестных два 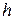 и
и 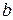 , поэтому сами задаем отношение
, поэтому сами задаем отношение 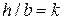 . Зная
. Зная 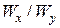 по (7.8) вычисляем необходимый
по (7.8) вычисляем необходимый 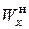 , а по нему размеры
, а по нему размеры 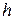 и
и 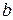 с учетом отношения
с учетом отношения 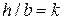 . При подборе стандартных двутавров и швеллеров аналогично: если
. При подборе стандартных двутавров и швеллеров аналогично: если 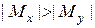 сечение располагаем вертикально, как в таблицах ГОСТа и берем: для двутавров
сечение располагаем вертикально, как в таблицах ГОСТа и берем: для двутавров 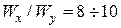 , для швеллеров
, для швеллеров 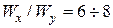 ; если
; если 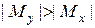 сечение располагаем горизонтально и для двутавров
сечение располагаем горизонтально и для двутавров 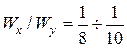 , для швеллеров
, для швеллеров 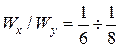 . Далее по (7.8) находимый необходимый
. Далее по (7.8) находимый необходимый 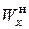 и по нему стандартный номер профиля (в первом случае
и по нему стандартный номер профиля (в первом случае 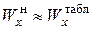 , во втором
, во втором 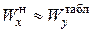 ). Определив номер профиля, делаем его проверку по первой формуле (7.8), подставляя табличные значения
). Определив номер профиля, делаем его проверку по первой формуле (7.8), подставляя табличные значения 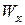 и
и 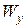 из ГОСТа с учетом вышеуказанного в скобках. Можно учесть
из ГОСТа с учетом вышеуказанного в скобках. Можно учесть 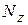 , добавив
, добавив 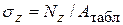 .
.
Для произвольного сечения условия прочности имеют вид 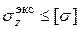 : надо найти наиболее удаленные от Н.О точки сечения, найти в них
: надо найти наиболее удаленные от Н.О точки сечения, найти в них 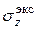 и сравнить их с допускаемыми.
и сравнить их с допускаемыми.
Для балок из хрупких материалов отдельно делается проверка прочности в растянутой (р) и сжатой (сж) зонах, т.к. для них 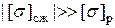 . Размеры произвольного сечения определяются методом попыток (подбором). При каждой попытке необходимо уточнить положение Н.О и координаты точек сечения с
. Размеры произвольного сечения определяются методом попыток (подбором). При каждой попытке необходимо уточнить положение Н.О и координаты точек сечения с 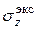 .
.
Определение прогибов
Определяют закон изменения прогибов 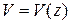 в плоскости
в плоскости 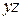 как указано в разделе 5, используя известное уравнение
как указано в разделе 5, используя известное уравнение 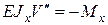 и метод Клебша. Далее определяют прогибы
и метод Клебша. Далее определяют прогибы 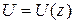 в горизонтальной плоскости
в горизонтальной плоскости 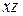 используя метод Клебша и аналогичное уравнение
используя метод Клебша и аналогичное уравнение 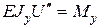 . Полный прогиб «
. Полный прогиб «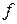 » в любом сечении балки найдем геометрическим сложеним прогибов
» в любом сечении балки найдем геометрическим сложеним прогибов 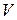 и
и 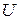 в каждом сечении:
в каждом сечении: 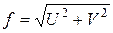 . Вычислив «
. Вычислив «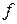 » в нескольких сечениях по длине балки, строят изогнутую ось балки и проверяют ее жесткость.
» в нескольких сечениях по длине балки, строят изогнутую ось балки и проверяют ее жесткость.
 2015-01-30
2015-01-30 936
936








