Постановка задачи. Рассмотрим однородную изотропную цилиндрическую стенку с внутренним радиусом 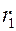 и наружным –
и наружным – 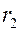 . Коэффициент теплопроводности материала стенки
. Коэффициент теплопроводности материала стенки 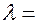 const.
const.
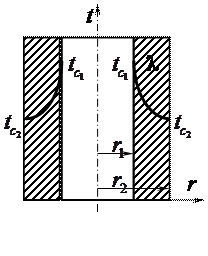 На внутренней поверхности стенки поддерживается температура
На внутренней поверхности стенки поддерживается температура 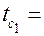 const, а на наружной –
const, а на наружной – 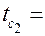 const (т.е. заданы граничные условия первого рода). Высота стенки (по оси z) бесконечно большая. В этих условиях температурное поле
const (т.е. заданы граничные условия первого рода). Высота стенки (по оси z) бесконечно большая. В этих условиях температурное поле 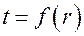 будет одномерным. Необходимо найти закон изменения температуры
будет одномерным. Необходимо найти закон изменения температуры 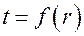 , плотность теплового потока и тепловой поток через цилиндрическую стенку.
, плотность теплового потока и тепловой поток через цилиндрическую стенку.
Для нахождения температурного поля 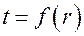 запишем дифференциальное уравнение теплопроводности в цилиндрических координатах, учитывая, что ¶t/¶t = 0, так как задача стационарная.
запишем дифференциальное уравнение теплопроводности в цилиндрических координатах, учитывая, что ¶t/¶t = 0, так как задача стационарная. 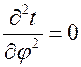 и
и 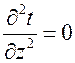 (температура по полярному углу и высоте стенки не изменяется).
(температура по полярному углу и высоте стенки не изменяется).
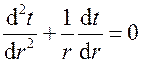 .
.
Для решения уравнения (1.30) обозначим 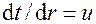 , тогда
, тогда 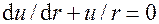 . Разделяя переменные
. Разделяя переменные 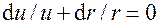 и интегрируя, получаем
и интегрируя, получаем 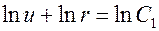 , или
, или 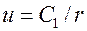 . Возвращаясь к первоначальной переменной
. Возвращаясь к первоначальной переменной 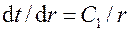 , разделяя переменные и интегрируя, получим общее решение уравнения (1.30)
, разделяя переменные и интегрируя, получим общее решение уравнения (1.30)
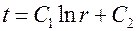 .
.
Для определения постоянных интегрирования 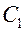 и
и 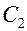 запишем граничные условия:
запишем граничные условия:
при 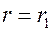
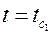 ,
, 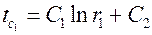 ,
,
при 
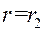
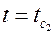 ,
, 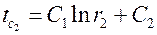 .
.
Решая систему, находим 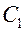 и
и 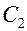 , подстановка значений которых позволяет получить закон изменения температуры по толщине цилиндрической стенки:
, подстановка значений которых позволяет получить закон изменения температуры по толщине цилиндрической стенки: 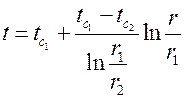 .
.
Видно, что температура в стенке изменяется по логарифмическому закону.
Тепловой поток через цилиндрическую стенку длиной l можно найти по закону Фурье 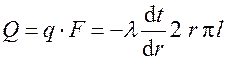 .
.
Производная 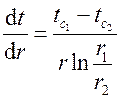 . Тогда
. Тогда 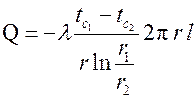 или после сокращения на текущий радиус r и умножения числителя и знаменателя на минус единицу получим
или после сокращения на текущий радиус r и умножения числителя и знаменателя на минус единицу получим
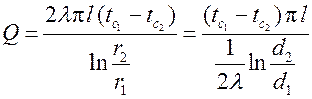 .
.
Тепловой поток, отнесенный к единице длины цилиндрической стенки (трубы), называется линейной плотностью теплового потока и обозначается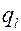 , Вт/м:
, Вт/м:
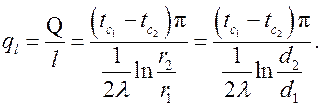
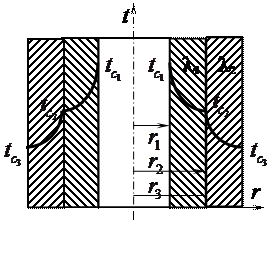 Многослойная стенка
Многослойная стенка
В случае многослойной цилиндрической стенки с идеальным контактом между соприкасающимися слоями (выполняются граничные условия четвертого рода), для каждого слоя, если их n, линейную плотность теплового потока можно найти по полученной формуле. Выразив разность температур и сложив полученные значения
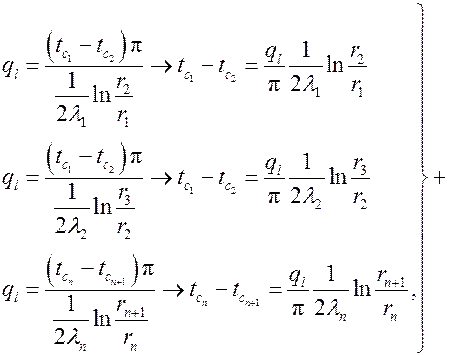
получим
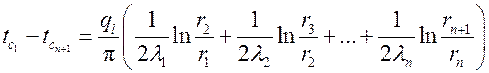 ,
,
откуда
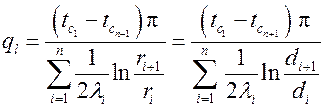 .
.
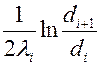 называется термическим сопротивлением теплопроводности i -го слоя цилиндрической стенки.
называется термическим сопротивлением теплопроводности i -го слоя цилиндрической стенки.
 2014-04-09
2014-04-09 651
651








