2015-01-30
609
| Год |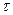 
| 
| 
| 
| 
| 
| 
|
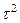
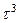
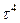
| Сумма |
Решая систему уравнений для определения параметров линейной функции:
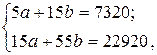получаем: 
Линейная функция, аппроксимирующая динамический ряд, имеет следующий вид:
.
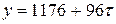Соответственно, прогноз продаж автомобилей на 2006 год:
.
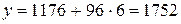Результаты предварительных расчётов среднего квадратического отклонения сведём в таблицу 3.4.
Среднее квадратическое отклонение от линейного тренда:
.
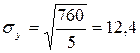Ширина доверительного интервала (при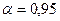 
):
.
Интервальный прогноз: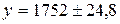 
или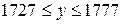 
.
Таблица 3.4
Предварительные расчеты среднего квадратического отклонения от линейного тренда
| № | Год | Количество проданных автомобилей, шт.,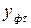 
| Вид уравнения | |
| ||||
| 
| |||
|
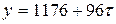
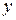
Для параболы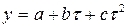 
система уравнений, решая которую необходимо определить коэффициенты 
, 
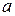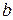и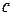 
, имеет вид:
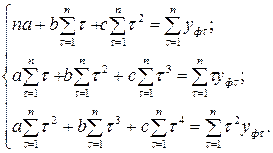
После подстановки расчётных значений имеем:
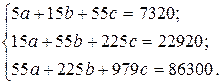
Решая данную систему уравнений, получаем:
, 
, 
.
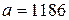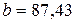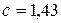Парабола, аппроксимирующая динамический ряд, имеет следующий вид:
Соответственно, прогноз продаж автомобилей на 2006 год:
.
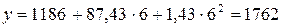Результаты предварительных расчетов среднего квадратического отклонения сведём в таблицу 3.5.
Таблица 3.5
Предварительные расчеты среднего квадратического отклонения
от параболического тренда
| № | Год | Количество проданных автомобилей, шт.,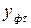
| Вид уравнения | |
| ||||
|
|
| |||
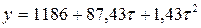
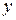
| 1274,9 | ||||
| 1366,6 | 275,6 | |||
| 1461,2 | 353,4 | |||
| 1558,6 | ||||
| 1658,9 | 1,2 | |||
|
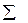
| 730,2 |
Среднее квадратическое отклонение от параболического тренда:
.
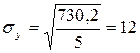Ширина доверительного интервала (при ):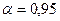 
.
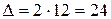Интервальный прогноз: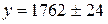 
или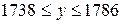 
.
Таким образом, прогноз на 2006 год, при аппроксимации предложенного динамического ряда линейной функцией, будет иметь следующий вид: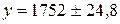 
, а при аппроксимации параболической функцией: .
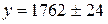Другим типом задач, решаемых с помощью аппроксимации, являются задачи определения рациональных сроков эксплуатации исследуемых объектов.
Пример. В таблице 3.6 приведены показатели, характеризующие состояние водопроводных сетей города Пскова. Анализ данных показателей позволяет сделать вывод, что с ростом срока службы водопроводных сетей увеличивается количество аварий, растут объемы утечек воды по причине изношенности.
Таблица 3.6
Состояние сетей водопровода
| Параметры | Срок эксплуатации водопроводных сетей, лет | |||||
| до 15 | 15-19 | 20-24 | 25-29 | 30-34 | Старше 34 | |
| Протяжённость, км | 52,9 | 63,1 | 62,3 | 33,8 | 31,6 | |
| Количество аварий на 1 км, шт. | 0,9 | 0,8 | 1,4 | 1,9 | 2,5 | 3,2 |
| Процент потерь в связи с износом, % | ||||||
| Потери от утечки воды, тыс.руб. на 1км сетей | 22,161 | 44,322 | 66,483 | 97,508 | 132,966 | 177,28 |
| Затраты на аврийно-восстан. работы, тыс.руб | 6,1 | 16,24 | 28,42 | 38,57 | 50,75 | 64,96 |
| Общие затраты на 1км сетей тыс.руб. | 28,261 | 60,562 | 94,903 | 136,078 | 183,716 | 242,24 |
Необходимо определить рациональный срок службы сетей, если единовременные затраты на замену 1 км водопровода составляют 1400 тыс. руб., а нормативный коэффициент эффективности капитальных вложений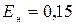 
.
Решение:
Условием для определения рационального срока службы сетей будем считать равенство потерь, связанных с износом сетей и приведенных единовременных затрат на их замену:
,
где 
- потери, связанные с утечкой воды;
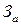- затраты на аварийно-восстановительные работы;
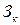- единовременные затраты на замену участка водопровода.
Аппроксимируем зависимость общих потерь, связанных с износом водопроводных сетей параболической зависимостью:
,
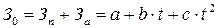здесь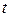 
- нормированный срок эксплуатации водопровода, единица которого
соответствует периоду 5 лет.
Результаты предварительных расчетов эмпирических коэффициентов сведём в таблицу 3.7
Таблица 3.7
