В последнее время использованию оптимизационных моделей для решения экономико-управленческих задач уделяется достаточно много внимания. В первую очередь это связано с развитием средств вычислительной техники, которая позволяет произвести вычисления параметров достаточно быстро.
Оптимизационная модель представляет собой модель математического программирования, состоящую из целевой функции и системы ограничений в форме уравнений или неравенств. Достоинством оптимизационных моделей является то, что они направлены на поиск наиболее эффективного (оптимального) управленческого решения при соблюдении установленных ограничений.
Целевая функция описывает цель оптимизации и представляет собой зависимость показателя, по которому ведётся оптимизация, от искомых переменных. На макроуровне критерием оптимальности может являться максимум валового национального дохода, максимум среднедушевого денежного дохода. На микроуровне: максимум прибыли предприятия, минимум затрат и др.
Например, общий вид модели для расчёта оптимального варианта производства продукции на предприятии:
Целевая функция: 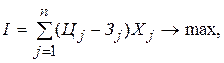
Система ограничений:
ограничения по сбыту 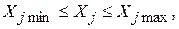
ограничения по мощности 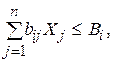
ограничения по снабжению 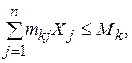
условие неотрицательности 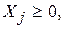
где 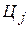 - цена реализации единицы товара
- цена реализации единицы товара  -го вида;
-го вида;
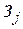 - затраты на изготовление единицы товара
- затраты на изготовление единицы товара 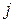 -го вида;
-го вида;
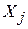 - количество товара
- количество товара 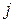 -го вида, подлежащее изготовлению;
-го вида, подлежащее изготовлению;
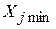 - обязательный минимальный объём производства товара
- обязательный минимальный объём производства товара 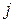 -го вида, обусловленный необходимостью выполнения уже заключённых договоров или необходимостью сохранения своего присутствия с минимальным предложением на рынках, привлекательных в долгосрочном периоде;
-го вида, обусловленный необходимостью выполнения уже заключённых договоров или необходимостью сохранения своего присутствия с минимальным предложением на рынках, привлекательных в долгосрочном периоде;
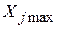 - максимально возможный объём реализации товара
- максимально возможный объём реализации товара 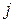 -го вида;
-го вида;
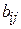 - норма затрат времени по изготовлению единицы товара
- норма затрат времени по изготовлению единицы товара 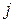 -го вида на оборудовании
-го вида на оборудовании 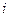 -го вида;
-го вида;
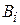 - фонд рабочего времени на оборудовании
- фонд рабочего времени на оборудовании 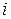 -го вида;
-го вида;
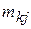 - норма затрат материала
- норма затрат материала 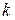 -го вида на изготовление единицы товара
-го вида на изготовление единицы товара 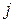 -го вида;
-го вида;
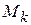 - имеющийся фонд
- имеющийся фонд 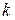 -го вида сырья.
-го вида сырья.
Область практического применения оптимизационных моделей ограничена «жёсткой» схемой их построения. Например, на практике фонд рабочего времени 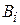 , при необходимости можно увеличить за счет выхода на работу в выходные дни. Таким образом, ограничение по мощности изменится, и оптимальное решение уже будет иным.
, при необходимости можно увеличить за счет выхода на работу в выходные дни. Таким образом, ограничение по мощности изменится, и оптимальное решение уже будет иным.
Пример. Предприятие выпускает продукцию двух видов: А и Б. Исходные данные о выпускаемой продукции представлены в таблице 5.1.
Таблица 5.1
Данные о продукции предприятия
| Характеристика | Продукция | |
| А | Б | |
| Маржинальная прибыль, руб./шт. | ||
| Штучно-калькуляционное время, мин. | ||
| Максимально возможный объём продаж, шт. | ||
| Фонд рабочего времени, час. |
Определить объёмы выпуска продукции вида А и вида Б, максимизирующие прибыль предприятия.
Решение:
Обозначим искомые объёмы выпуска продукции 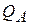 и
и 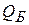 .
.
Тогда целевая функция, направленная на поиск решения, максимизирующего маржинальную прибыль предприятия, будет иметь следующий вид: 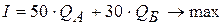 .
.
На искомые объемы выпуска продукции накладываются ограничения по максимальным объёмам продаж: 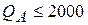 ;
; 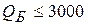 , а также ограничение по фонду рабочего времени, который составляет
, а также ограничение по фонду рабочего времени, который составляет 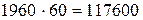 мин.:
мин.: 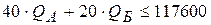 . Таким образом, оптимизационная модель запишется следующим образом:
. Таким образом, оптимизационная модель запишется следующим образом:
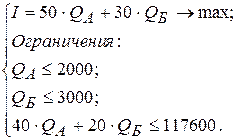
Данную задачу можно решить графическим и аналитическим методами. Кроме того, в некоторых программных продуктах, например в EXCEL, встроены алгоритмы, позволяющие строить оптимизационные модели в диалоговом режиме.
Решение оптимизационных задач графическим методом рассмотрено в достаточно большом количестве учебных пособий. Графический метод позволяет наглядно определить оптимальные значения искомых параметров, если их количество не более двух.
При аналитическом подходе к решению задачи можно отметить, что объёмы выпускаемой продукции лимитирует фонд рабочего времени. Прибыль на единицу рабочего времени при изготовлении изделий вида А и вида Б составляет: 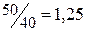 руб./мин., и
руб./мин., и 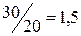 руб./мин., соответственно. Так как изготовление изделия Б приносит больше прибыли на единицу рабочего времени, то необходимо изготовить 3000 изделий вида Б (трудоёмкость данной работы составляет
руб./мин., соответственно. Так как изготовление изделия Б приносит больше прибыли на единицу рабочего времени, то необходимо изготовить 3000 изделий вида Б (трудоёмкость данной работы составляет 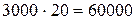 мин.). А оставшееся рабочее время (117600-60000=57600 мин.) затратить на изготовление изделий вида А:
мин.). А оставшееся рабочее время (117600-60000=57600 мин.) затратить на изготовление изделий вида А: 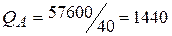 .
.
Ответ: 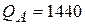 ,
, 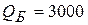 .
.
При решении данной задачи мы исходили из «жёсткого» ограничения по фонду рабочего времени, чего на практике, как правило, не бывает. Работодатель имеет возможность увеличения фонда рабочего времени за счёт работы в две смены и в выходные дни. Поэтому, несмотря на то, что примерам поиска оптимальных объёмов производства при помощи линейных оптимизационных моделей в литературе уделено достаточно много внимания, практика решения подобных задач весьма ограничена.
Гораздо большее применение нашли на практике оптимизационные задачи на определение оптимальной структуры (примеры которых приведены ниже в заданиях) и стохастические (вероятностные) модели.
Пример. Предприятие выпускает продукцию пяти видов. Статистические данные об объёмах реализации продукции приведены в таблице 5.2.
Таблица 5.2
Объёмы реализации продукции, шт.
| Вид продукции | Месяц | ||||
| январь | февраль | март | апрель | май | |
| А | |||||
| Б | |||||
| В | |||||
| Г | |||||
| Д |
Цена продукции и переменные затраты на её изготовление приведены в таблице 5.3. Определить сколько продукции каждого вида следует изготовить в июне месяце, если производственный бюджет предприятия – 300000 рублей.
Таблица 5.3
Цена и затраты на изготовление продукции, руб./шт.
| Показатель | Продукция | ||||
| А | Б | В | Г | Д | |
| Цена | |||||
| Переменные затраты |
Решение:
Используя данные, приведенные в таблице 5.2, определим параметры, описывающие вероятностный характер продаж продукции: среднее арифметическое значение - 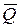 и среднеквадратическое отклонение -
и среднеквадратическое отклонение - 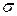 .
.
Для изделия А среднее арифметическое значение составит:
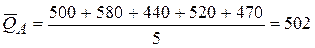 ,
,
Среднеквадратическое отклонение:
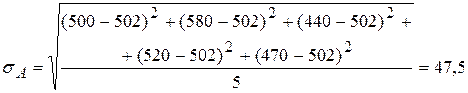 .
.
Аналогично рассчитаем значения данных параметров по остальным видам продукции. Результаты расчётов сведём в таблицу 5.4.
С вероятностью 99,9% (согласно правилу 3 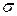 ) можно говорить о том, что значение объема продаж попадает в интервал:
) можно говорить о том, что значение объема продаж попадает в интервал: 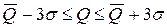 .
.
Определим для изделия А предельное минимальное значение объёма продаж. Вероятность реализации объёма продукции, находящегося в интервале 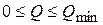 , составляет - 1 (100%). А также предельное максимальное значение. Вероятность реализации объёма продукции, находящегося в интервале
, составляет - 1 (100%). А также предельное максимальное значение. Вероятность реализации объёма продукции, находящегося в интервале 
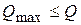 , равна нулю:
, равна нулю:
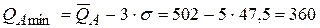 ;
;
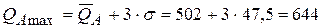 .
.
Аналогично рассчитаем предельные значения для остальных видов продукции. Результаты расчётов сведём в таблицу 5.4.
Таблица 5.4
Результаты расчёта статистических характеристик
| Показатель | Продукция | ||||
| А | Б | В | Г | Д | |
| Среднее арифметическое значение, шт. | |||||
| Среднеквадратическое отклонение, шт. | 47,5 | 30,6 | 44,5 | 57,4 | 7,1 |
| Предельное минимальное значение, шт. | |||||
| Предельное максимальное значение, шт. |
Будем считать, что вероятность реализации продукции описывается равновероятным законом распределения (рис.5.1).
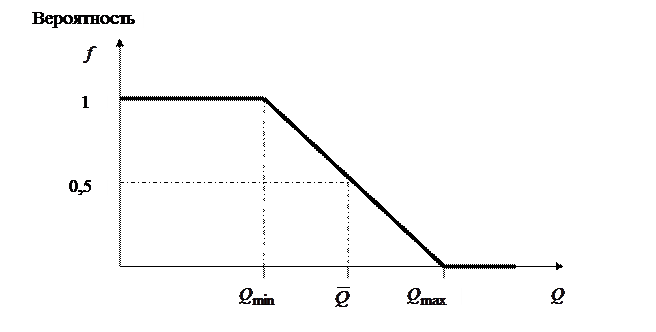
Рис. 5.1. Зависимость вероятности реализации продукции от объёмов
изготовления.
Тогда вероятность реализации продукта можно описать в следующем виде:
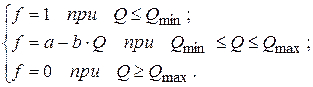
Учитывая, что производство продукции минимизируется бюджетом, определим затраты на производство продукции при минимальном и максимальном объёмах производства:
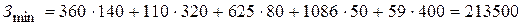 руб.;
руб.;
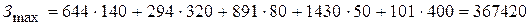 руб.
руб.
Так как производственный бюджет находится в пределе 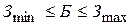 (
(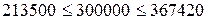 ), значения объёмов производства, максимизирующих прибыль, находятся в интервале
), значения объёмов производства, максимизирующих прибыль, находятся в интервале 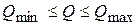 . Вероятность реализации объёма продукции в данном интервале описывается зависимостью
. Вероятность реализации объёма продукции в данном интервале описывается зависимостью 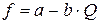 .
.
Параметры 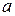 и
и 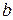 определим из условий:
определим из условий:

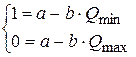
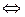
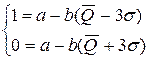
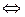
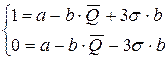
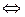
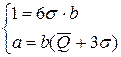
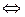
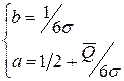 .
.

 Для изделия А имеем:
Для изделия А имеем:
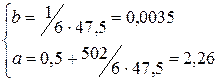
Аналогично рассчитаем коэффициенты линейной зависимости для остальных видов продукции. Результаты расчётов сведём в табл. 5.5. Маржинальную прибыль от реализации единицы продукции определим по формуле:
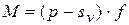 ,
,
где 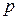 и
и 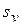 - цена реализации и переменные затраты, соответственно;
- цена реализации и переменные затраты, соответственно;
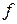 - вероятность реализации продукции.
- вероятность реализации продукции.
Таблица 5.5
Результаты расчета коэффициентов
| Параметр | Продукция | ||||
| А | Б | В | Г | Д | |
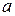 | 2,262 | 1,6 | 3,342 | 4,152 | 2,386 |
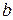 | 0,0035 | 0,0054 | 0,0037 | 0,0029 | 0,0236 |
В диапазоне 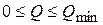 вероятность продаж каждого изделия
вероятность продаж каждого изделия 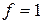 , следовательно, ожидаемая маржинальная прибыль от реализации объёма соответствующего
, следовательно, ожидаемая маржинальная прибыль от реализации объёма соответствующего 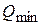 составит:
составит: 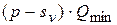 .
.
В диапазоне 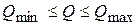 вероятность продаж изделия описывается линейной зависимостью
вероятность продаж изделия описывается линейной зависимостью 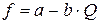 , следовательно, ожидаемая прибыль от реализации одного изделия составит:
, следовательно, ожидаемая прибыль от реализации одного изделия составит: 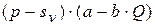 , а прибыль от реализации
, а прибыль от реализации 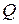 изделий:
изделий: 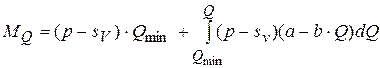 .
.
Таким образом, целевая функция, максимизирующая маржинальную прибыль от реализации товаров будет иметь следующий вид:
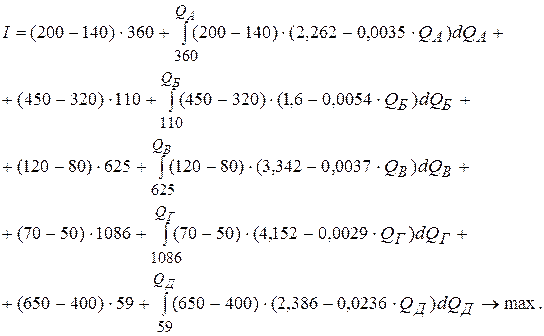
Последовательно преобразуем целевую функцию:
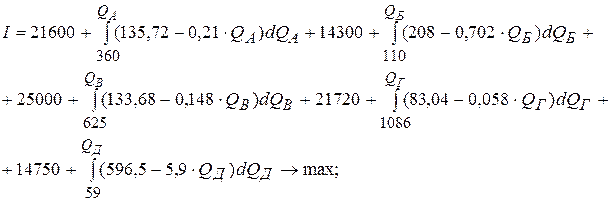
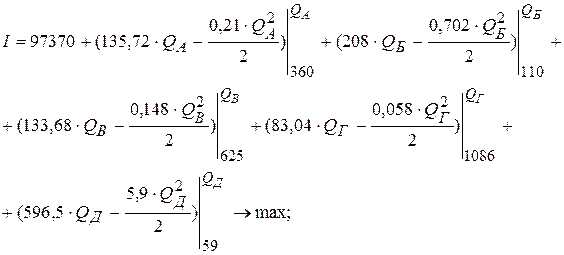
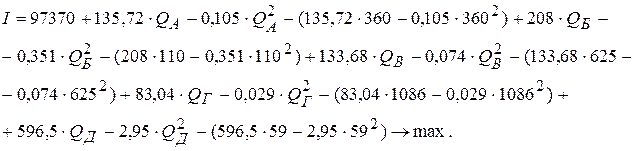
После преобразований оптимизационная модель будет иметь следующий вид:
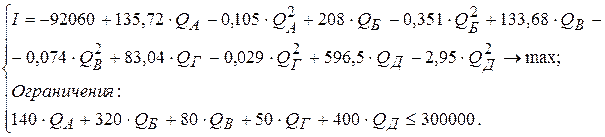
Для решения полученной оптимизационной модели воспользуемся программным продуктом EXCEL. Для искомых значений объёмов продаж  определим адреса ячеек А1…А5 в которых будут находиться их текущие значения. Целевая функция будет считаться в ячейке С1 (рис.5.2). Затраты на производство продукции в ячейке Е1 (рис.5.3).
определим адреса ячеек А1…А5 в которых будут находиться их текущие значения. Целевая функция будет считаться в ячейке С1 (рис.5.2). Затраты на производство продукции в ячейке Е1 (рис.5.3).
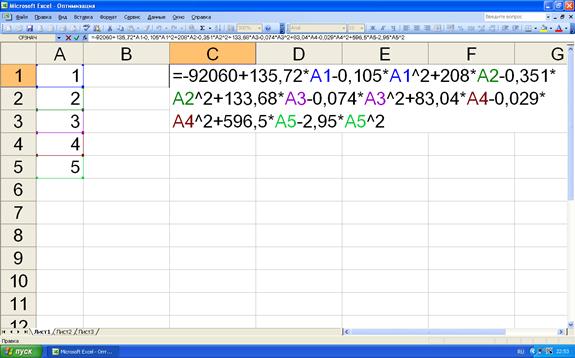
Рисунок 5.2. Запись целевой функции в программе EXCEL.
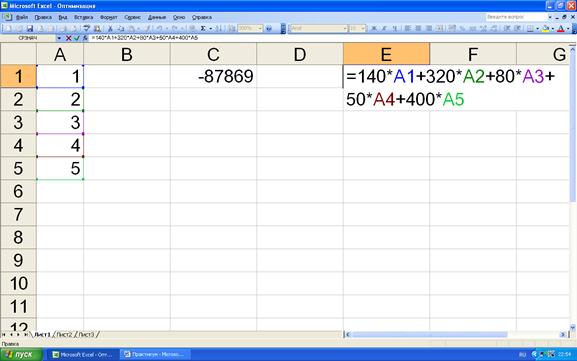
Рисунок 5.3. Запись ограничения в программе EXCEL.
Далее выберем в диалоговом меню «сервис» и функцию «поиск решения». Если функция «поиск решения» не установлена, то выберем «надстройки» и установим данную функцию. В диалоговом окне функции «поиск решения» установим целевую ячейку С1 равной максимальному значению, изменяя ячейки А1…А5 (рис.5.4).
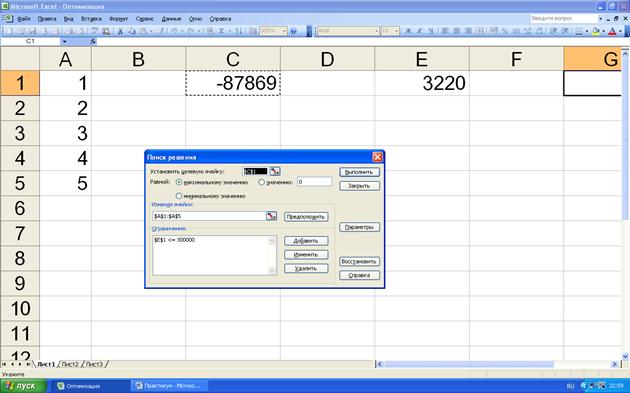
Рисунок 5.4. Вызов функции «поиск решения».
В окне меню ограничения выберем функцию «добавить». Сошлемся на ячейку Е1 и установим для её значения соответствующее ограничение (рис.5.5).
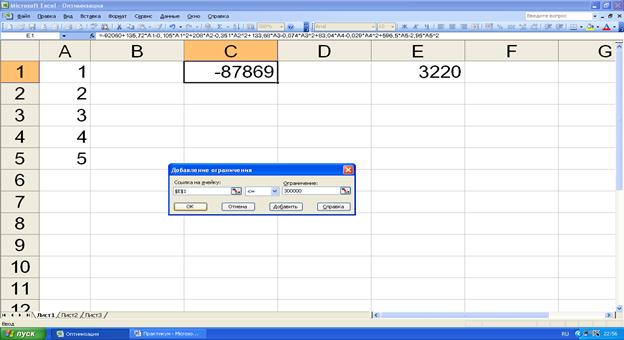
Рисунок 5.5. Диалоговое окно опции «добавить ограничение».
Далее нажмём кнопку «ОК» и вернёмся в меню функции «поиск решения» (рис.5.4). Нажмём кнопку «Выполнить». В ячейках А1…А5 появляются значения оптимальных объёмов продаж (рис.5.6).
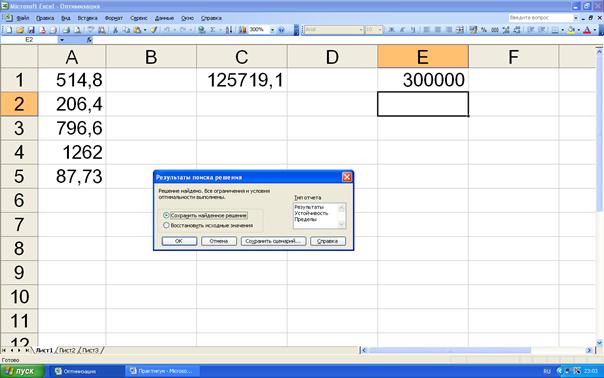
Рисунок 5.6. Результаты поиска оптимального решения.
Ответ: 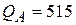 ;
; 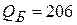 ;
;  ;
; 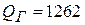 ;
; 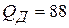 .
.
Тема 6. Нормативный метод планирования
Нормативный метод используется для определения потребности в ресурсах путём умножения норм на соответствующие объёмные показатели. Норма – это мера (количество) затрат ресурса на изготовление единицы продукции в конкретных производственно-технических условиях.
Нормативный метод самый простой в применении метод планирования. Например, если норма затрат времени на изготовление изделия – 2 часа, а объём производства – 1000 шт., то трудоёмкость изготовления 1000 изделий составит: 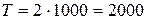 часов.
часов.
Основная сложность при использовании нормативного метода состоит в определении величины нормы. В данном пособии рассматриваются примеры расчёта норм аналитически-расчётным и отчётно-статистическим методами.
Аналитически-расчётный метод основан на разделении выполняемых работ на составные элементы с последующим их анализом и проектированием рациональных вариантов использования ресурсов.
Пример. Из стального прутка длиной 3 метра отрезным резцом с шириной 3 мм нарезаются заготовки длиной 70 мм. Масса одного погонного метра прутка – 2,4 кг. Процент выхода из заготовок готовых деталей составляет - 95%. Определить норму затрат материала на изготовление детали.
Решение. Определим количество заготовок, изготавливаемых из одного прутка длиной 3 м (3000 мм), с учётом ширины распила - 3 мм. Будем считать, что длина прутка, закреплённого в шпинделе станка, составляет 100 мм. Тогда количество заготовок, нарезаемых из прутка, будет равно:
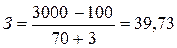 , т.е. 39 заготовок.
, т.е. 39 заготовок.
Учитывая потери материала по причине брака при изготовлении деталей из заготовок, определим ожидаемое количество годных деталей, получаемых из одного прутка:
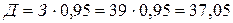 дет.
дет.
Норма затрат материала составит:
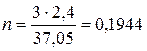 кг/дет.
кг/дет.
Данная норма используется в том случае, когда цена на материал установлена в рублях за 1 кг. Если цена на материал установлена в рублях за метр погонный, то соответственно, норма составит:
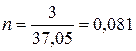 м.пог/дет.
м.пог/дет.
Более сложной является задача определения нормы, если из одного и того же материала изготавливаются две (и более) детали, входящие в одно изделие.
Пример. При изготовлении ученической парты (рис 6.1) из прутка длиной 3 м нарезаются 4 заготовки вида А, длиной 80 см и 4 заготовки вида Б, длиной 52 см.
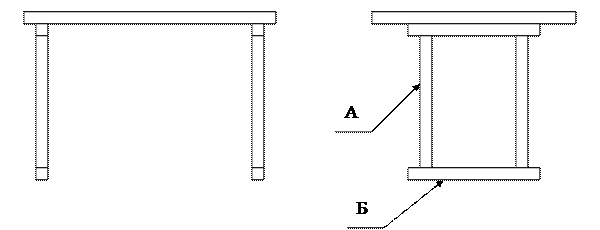
Рисунок 6.1. Конструкция ученической парты.
Масса одного метра погонного прутка составляет 1,4 кг. Определите норму затрат прутка на изготовление парты.
 2015-01-30
2015-01-30 1595
1595








