Экономико-статистические модели представляют собой вид моделей, описывающих с помощью уравнений регрессии зависимости между влияющими факторами и результирующим фактором. Различают однофакторные и многофакторные модели. Многофакторные модели позволяют изучать влияние на объект прогнозирования нескольких факторов, однофакторные – одного. На практике наибольшее применение нашли экономико-статистические модели линейного вида:
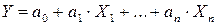 ,
,
где 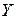 - результирующий фактор;
- результирующий фактор;
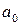 ,
, 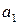 , …
, … 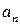 - эмпирические коэффициенты;
- эмпирические коэффициенты;
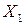 , …
, … 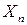 - влияющие факторы.
- влияющие факторы.
Для определения значений эмпирических коэффициентов обычно используется метод наименьших квадратов (см. тему 3). Рассмотрим процедуру разработки многофакторной экономико-статистической модели на следующем примере.
Пример. Необходимо построить экономико-статистическую модель зависимости объёма выпускаемой продукции на предприятиях, работающих в одной отрасли, от составляющих ресурсного потенциала: численности работников, оборотных и основных средств. Исходные данные приведены в таблице 4.1.
Таблица 4.1
| Наименование предприятия | Численность работников, чел. | Основные средства, млн. руб. | Оборотные средства, млн.руб. | Объём выпускаемой продукции, млн.руб |
| ООО «Конструктор» | ||||
| ООО «Заря» | ||||
| ООО «Механик» | ||||
| ООО «Инженер» | ||||
| ООО «Инноватор» | ||||
| ООО «Исследователь» |
Решение:
При построении экономико-статистической модели будем исходить из предположения, что зависимость между результирующим фактором (объёмом выпускаемой продукции - 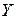 ) и влияющими факторами (численность работников -
) и влияющими факторами (численность работников - 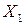 , основные средства -
, основные средства - 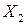 , оборотные средства -
, оборотные средства - 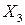 ) имеет линейный вид:
) имеет линейный вид:
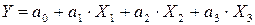 .
.
Система уравнений, в результате решения которой будут определены эмпирические коэффициенты, будет следующей:
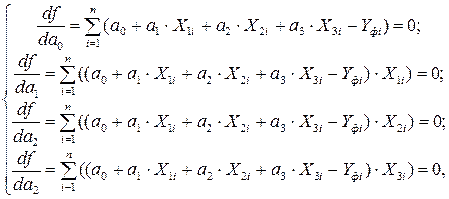
или
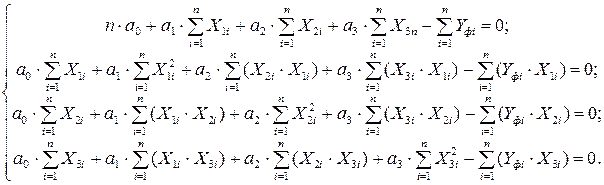
Промежуточные расчёты эмпирических коэффициентов сведем в таблицу 4.2.
Таблица 4.2а
Промежуточные расчёты коэффициентов
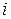 | 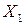 | 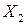 | 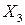 | 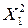 | 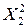 | 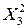 | 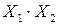 | 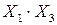 | 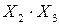 |
 |
Таблица 4.2б
Промежуточные расчёты коэффициентов
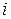 | 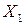 | 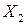 | 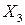 | 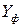 | 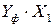 | 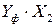 | 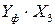 |
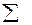 |
После подстановки результатов промежуточных расчётов в систему уравнений, имеем:
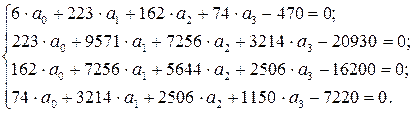
Можно решать данную систему уравнений так, как это было показано в предыдущем параграфе. А можно воспользоваться программным продуктом EXCEL.
Вариант 1. Запишем данную систему в матричном виде:
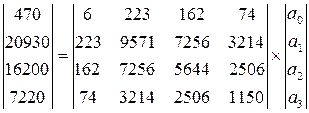 .
.
Тогда вектор-столбец эмпирических коэффициентов равен:
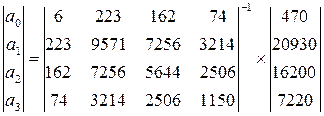 .
.
Для расчёта обратной матрицы занесем исходную матрицу в ячейки (рисунок 4.1).
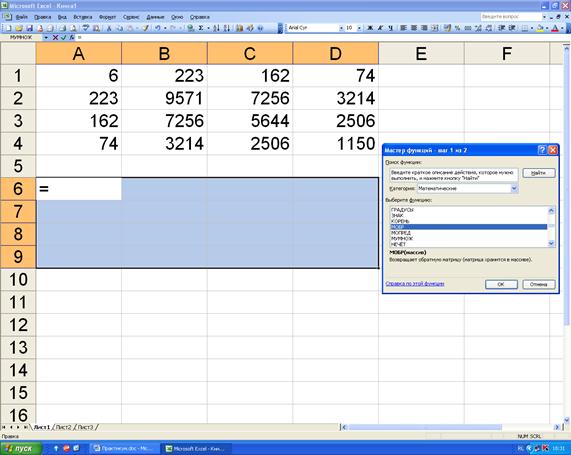
Рисунок 4.1. Вызов функции расчёта обратной матрицы.
Выделим ячейки, в которые будут помещены коэффициенты обратной матрицы (так как размерность матрицы в нашем случае 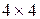 , то выделяем массив
, то выделяем массив 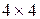 - A6:D9). Функция «определить матрицу обратную данной» относится к категории «математические функции». Нажмём кнопку
- A6:D9). Функция «определить матрицу обратную данной» относится к категории «математические функции». Нажмём кнопку 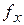 и далее категорию «математические функции» и выберем функцию «МОБР» - расчёт обратной матрицы
и далее категорию «математические функции» и выберем функцию «МОБР» - расчёт обратной матрицы
Диалоговое окно функции «МОБР» приведено на рисунке 4.2. В строке «Массив» укажем массив ячеек, содержащих элементы исходной матрицы. После того как информация будет занесена, необходимо нажать на клавиатуре одновременно клавиши «Ctrl», «Shift» и «Enter». Результат расчёта обратной матрицы представлен на рисунке 4.3.
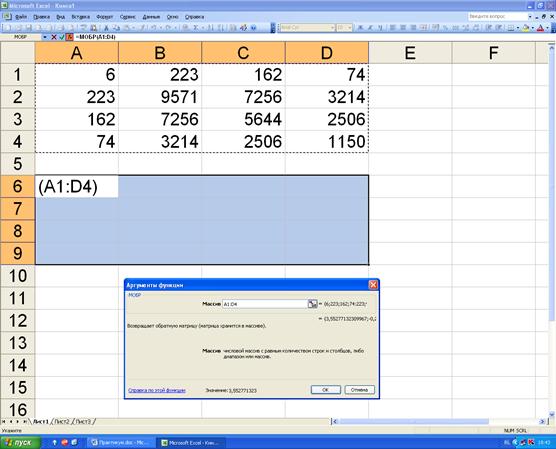
Рисунок 4.2. Диалоговое окно функции «МОБР».

Рисунок 4.3. Результат расчёта обратной матрицы.
Коэффициенты модели определим перемножив обратную матрицу на вектор-столбец значений результирующего фактора:
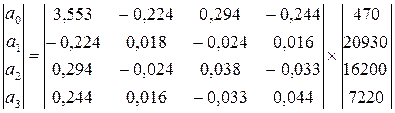 .
.
Выделим столбец ячеек (4 ячейки), в которые будут помещены значения коэффициентов. Откроем диалоговое окно функции «МУМНОЖ» в категории математических функций (рисунок 4.4). В массив 1 занесём адреса ячеек, содержащих значения коэффициентов обратной матрицы (А6:D9). В массив 2 - адреса ячеек, содержащих значения результирующего фактора.
Далее одновременно нажимаем клавиши «Ctrl», «Shift» и «Enter». На рисунке 4.5 представлен результат расчёта коэффициентов модели.

Рисунок 4.4. Диалоговое окно функции «МУМНОЖ».
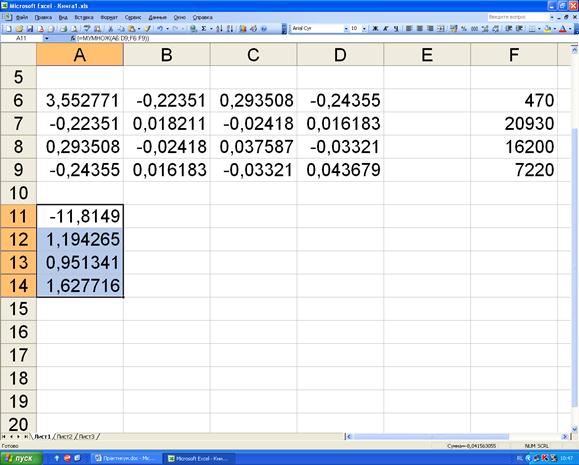
Рисунок 4.5. Результат расчёта коэффициентов модели.
Таким образом, экономико-статистическая модель зависимости объёма выпускаемой продукции от влияющих факторов будет следующей:
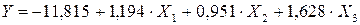 .
.
Вариант 2. Занесём исходные данные в ячейки. В диалоговом окне кликнем опцию «сервис - надстройки» и установим пакет анализа (рис. 4.6). После установки «Пакета анализа» снова кликнем опцию «сервис» и выберем операцию «анализ данных». В диалоговом окне операции «анализ данных» выберем инструмент анализа «регрессия».
На рисунке 4.7 показано диалоговое окно инструмента анализа «регрессия». В строке «Входной интервал Y» укажем адреса ячеек, содержащих значения результирующего фактора - $E$3:$E$8. В строке «Входной интервал Х» укажем адреса ячеек, содержащих значения влияющих факторов - $B$3:$D$8. В строке «Выходной интервал» укажем адреса ячеек, в которые будут внесены результаты расчётов.
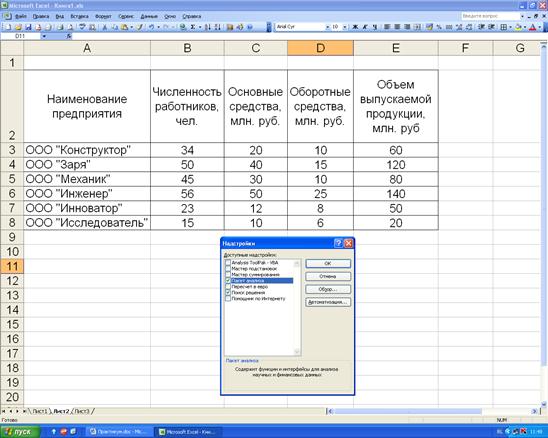
Рисунок 4.6. Установка Пакета анализа.
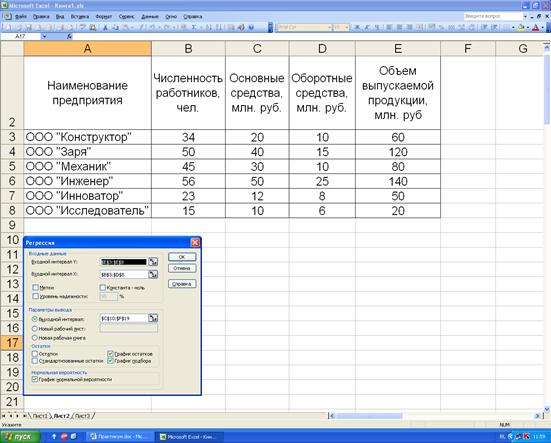
Рисунок 4.7. Диалоговое окно инструмента анализа – «регрессия».
Далее одновременно нажимаем клавиши «Ctrl», «Shift» и «Enter». На рисунке 4.8 представлен результат расчёта коэффициентов модели. Значения коэффициентов содержатся в ячейках I27-I30.
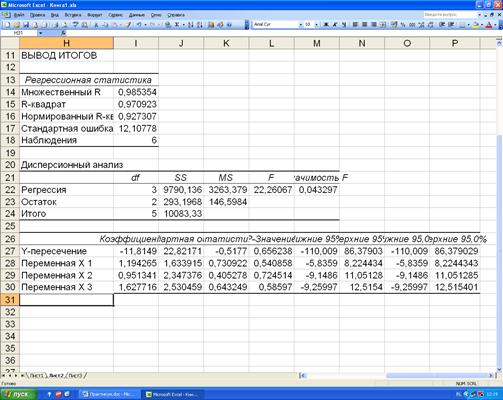
Рисунок 4.8. Результат расчёта коэффициентов модели в Пакете анализа.
Достоинством «Пакета анализа» является то, что он позволяет также получить качественную оценку полученной экономико-статистической модели.
После построения экономико-статистической модели определим отклонения теоретических значений от фактических, для чего подставим значения влияющих факторов 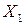 ,
, 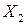 ,
, 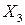 в экономико-статистическую модель. Например, для ООО «Конструктор» теоретическое значение результирующего фактора составит:
в экономико-статистическую модель. Например, для ООО «Конструктор» теоретическое значение результирующего фактора составит:
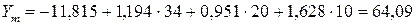 .
.
Отклонение теоретического значения результирующего фактора от фактического:
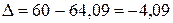 .
.
Результаты расчётов сведем в таблицу 4.3.
Таблица 4.3
Результаты расчётов по экономико-статистической модели
| Наименование предприятия | Теоретическое значение, 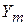 | Фактическое значение, 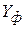 | Отклонение, 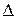 |
| ООО «Конструктор» | 64,09 | -4,09 | |
| ООО «Заря» | 110,37 | 9,63 | |
| ООО «Механик» | 86,74 | -6,74 | |
| ООО «Инженер» | 143,32 | -3,32 | |
| ООО «Инноватор» | 40,09 | 9,9 | |
| ООО «Исследователь» | 25,38 | -5,38 |
Анализируя данные, представленные в таблице 4.3, следует отметить, что с одной стороны отклонение теоретических значений результирующего фактора от фактических значений может носить случайный характер. С другой стороны вполне возможно, что предприятия ООО «Конструктор», ООО «Механик», ООО «Инженер», ООО «Исследователь» используют свой потенциал недостаточно эффективно.
Вывод о недостаточной эффективности использования ресурсного потенциала следует из следующих рассуждений. Теоретические значения результирующего фактора показывают величины объёмов выпускаемой продукции предприятиями при одинаковой средневзвешенной эффективности использования производственных ресурсов. Отклонения 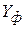 от
от 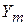 в меньшую сторону свидетельствуют об использовании ресурсов с меньшей степенью эффективности. И наоборот, превышение
в меньшую сторону свидетельствуют об использовании ресурсов с меньшей степенью эффективности. И наоборот, превышение 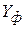 над
над 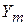 свидетельствует о том, что предприятия используют ресурсы более эффективно.
свидетельствует о том, что предприятия используют ресурсы более эффективно.
 2015-01-30
2015-01-30 1562
1562








