Графический способ (метод касательных). Применяют для логариф-мических или билогарифмических (сигмоидных) кривых титрования. Точка эквивалентности соответствует перегибу кривой, которую отождест-вляют с центром симметрии кривой титрования. Предполагается, что в окрестности точки эквивалентности кривая центральносимметрична. Для нахождения центра симметрии проводятся три прямые. Две прямые парал-лельны друг другу и являются касательными к некоторым участкам кривой титрования (рис. П.2). Чем ближе прямые будут находиться к точке экви-валентности, тем лучше. Третья прямая аппроксимирует точки около точки эквивалентности. Если получившийся отрезок АB разделить пополам, то найденная точка является искомой точкой эквивалентности, а ее абсцисса – эквивалентным объемом Vэкв. Если кривая несимметрична, то первую ка-сательную проводят к более крутому участку кривой титрования, а вторую –параллельно ей.
Недостатком метода является некоторая субъективность в определе-нии эквивалентного объема и невозможность рассчитать ошибку определе-ния Vэкв. Для определения доверительного интервала и относительной ошибки приходится проводить титрование параллельных проб.
Способ численного дифференцирования кривой титрования. Макси-мум дифференциальной кривой находится в точке эквивалентности (рис. П.3). Для каждой соседней пары точек вычисляется следующее отношение: (Еi+ 1 – Ei)/(V i+ 1 – V i), где Ei - потенциал ион-селективного электрода (или рН) после добавки титранта объемом Vi. Каждому вычис-ленному значению, а это будет ордината будущего графика, соответствует значение абсциссы, которая определяется как среднее арифметическое (V i+ 1 + V i)/2. Пример приведен в табл. П.3 и на рис. П.3.
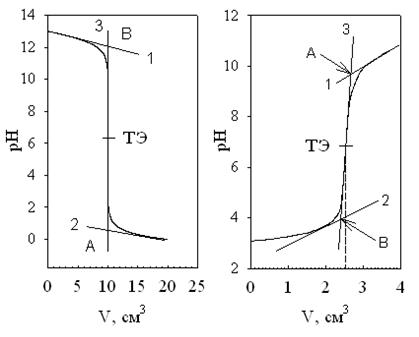
Рис. П.2. Кривые потенциометрического титрования
и их обработка методом касательных
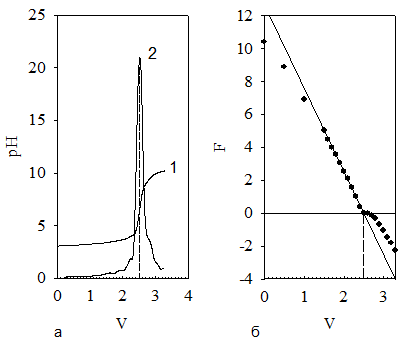
Рис. П.3. Кривая потенциометрического титрования
и ее обработка методом численного дифференцирования (а)
и методом Грана (б)
Таблица П.4
Результаты потенциометрического титрования
| № | V(титрант) | рН | (V i+ 1+V i)/2 | DV | DpH | DpH/DV | F |
| 0,0 | 3,08 | 0,25 | 0,5 | 0,07 | 0,14 | 10,39700 | |
| 0,5 | 3,15 | 0,75 | 0,5 | 0,11 | 0,22 | 8,88472 | |
| 1,0 | 3,26 | 1,25 | 0,5 | 0,14 | 0,28 | 6,92421 | |
| 1,5 | 3,40 | 1,55 | 0,1 | 0,05 | 0,50 | 5,03606 | |
| 1,6 | 3,45 | 1,65 | 0,1 | 0,05 | 0,50 | 4,49194 | |
| 1,7 | 3,50 | 1,75 | 0,1 | 0,05 | 0,50 | 4,00661 | |
| 1,8 | 3,55 | 1,85 | 0,1 | 0,07 | 0,70 | 3,57371 | |
| 1,9 | 3,62 | 1,95 | 0,1 | 0,08 | 0,80 | 3,04412 | |
| 2,0 | 3,70 | 2,05 | 0,1 | 0,08 | 0,80 | 2,53398 | |
| 2,1 | 3,78 | 2,15 | 0,1 | 0,13 | 1,30 | 2,10933 | |
| 2,2 | 3,91 | 2,25 | 0,1 | 0,19 | 1,90 | 1,56490 | |
| 2,3 | 4,10 | 2,35 | 0,1 | 0,42 | 4,20 | 1,01118 | |
| 2,4 | 4,52 | 2,45 | 0,1 | 1,68 | 16,80 | 0,38474 | |
| 2,5 | 6,20 | 2,55 | 0,1 | 2,00 | 20,00 | 0,00784 | |
| 2,6 | 8,20 | 2,65 | 0,1 | 0,80 | 8,00 | -0,02014 | |
| 2,7 | 9,00 | 2,75 | 0,1 | 0,40 | 4,00 | -0,12769 | |
| 2,8 | 9,40 | 2,85 | 0,1 | 0,33 | 3,30 | -0,32101 | |
| 2,9 | 9,73 | 2,95 | 0,1 | 0,19 | 1,90 | -0,68686 | |
| 3,0 | 9,92 | 3,05 | 0,1 | 0,14 | 1,40 | -1,06466 | |
| 3,1 | 10,06 | 3,15 | 0,1 | 0,09 | 0,90 | -1,47078 | |
| 3,2 | 10,15 | 3,25 | 0,1 | 0,10 | 1,00 | -1,81087 | |
| 3,3 | 10,25 | – | – | – | – | -2,28153 |
Линии 1 и 2 на рис. П.3а представляют собой соответственно инте-гральную и дифференциальную кривые титрования. Максимум на кривой 2 отвечает эквивалентному объему титранта 2,55 см3.
Безусловно, для нахождения точки эквивалентности асимметричных кривых титрования дифференциальный метод предпочтительней. Однако он имеет и негативные стороны. Во-первых, усложняется процедура расче-тов. Во-вторых, требуется большая частота экспериментальных точек в окрестности точки эквивалентности, что не всегда бывает удобно. Для определения доверительного интервала и относительной ошибки необхо-димо проводить титрование параллельных проб.
В настоящее время кривые титрования предварительно обрабатыва-ют (на ЭВМ) методом многоинтервального сглаживания с помощью полиномов невысокой степени (сплайнов), обеспечивающих сглаженность в точках разбиения, а также первой и второй производной.
Метод Грана. Основан на линеаризации кривой потенциометричес-кого (рН-метрического) титрования. Метод применяется при кислотно-основном титровании, когда титрантом является сильная кислота или силь-ное основание. В каждой точке титрования рассчитывается функция Грана
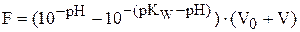 ,
,
где F – функция Грана; pKW – десятичный логарифм ионного произведения воды, взятый с обратным знаком; V0 – начальный объем титруемого рас-твора; V – объем добавленного титранта.
Точка эквивалентности – точка пересечения прямолинейных участ-ков линеаризованной кривой титрования с осью абсцисс при F = 0. Пример расчета для V0 = 125 см3 приведен в табл. П.4 и на рис. П.3б. Точка эквива-лентности соответствует объему титранта 2,50 см3.
Если титруются слабые кислоты или основания требуется довольно значительно перетитровать раствор, чтобы надежно провести линейную аппроксимацию кривой. Метод позволяет определить несколько точек экви-валентности при последовательном титровании, например, полипротонных кислот, их солей или смеси кислот.
Определение точки эквивалентности для сегментных (линейных) кривых титрования. Для сегментных (V-образных) кривых амперометри-ческого, кондуктометрического, спектрофотометрического титрования и др. точка эквивалентности является точкой излома кривых (рис. П.4). Точку излома находят аппроксимацией их квазилинейных участков (сегментов) прямыми линиями, которые экстраполируют до пересечения друг с другом. Для данных рис. П.4 аппроксимация проведена с помощью прикладного пакета Microsoft Excel. Уравнения регрессии приведены на графике, для нахождения точки эквивалентности решена система из двух линейных уравнений.

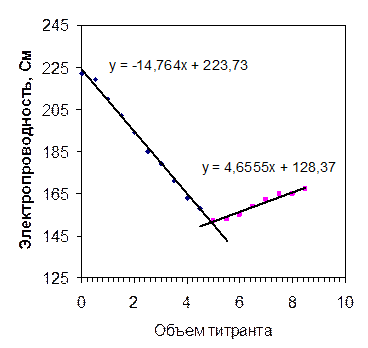
Рис. П.4. Сегментные (линейные) кривые титрования
Приложение 4
 2015-01-30
2015-01-30 15234
15234
