Возьмем на картографируемой поверхности окружность бесконечно малого радиуса и исследуем, как эта окружность будет изображаться в проекции.
 Известно, что масштаб длин в данной точке зависит от азимута
Известно, что масштаб длин в данной точке зависит от азимута  азимуту
азимуту  на картографируемой поверхности в проекции соответствует азимуту
на картографируемой поверхности в проекции соответствует азимуту  масштаб по этому направлению
масштаб по этому направлению 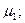 азимуту
азимуту 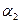 на поверхности соответствует в проекции азимут
на поверхности соответствует в проекции азимут 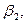 по этому направлению масштаб длин
по этому направлению масштаб длин 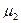 и т.д. (рис. 2.2).
и т.д. (рис. 2.2).
Рис. 2.2. Эллипс искажений
Из точки 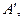 которая является изображением заданной на картографируемой поверхности точки
которая является изображением заданной на картографируемой поверхности точки 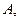 проведем направления, составляющие с направлением меридиана, принятым за ось
проведем направления, составляющие с направлением меридиана, принятым за ось 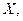 углы
углы 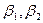 и т.д. На этих направлениях отложим отрезки, численно равные значениям масштаба длин
и т.д. На этих направлениях отложим отрезки, численно равные значениям масштаба длин 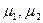 и т.д.
и т.д.
Соединив конечные точки этих отрезков, мы получим кривую, которая характеризует изменение масштаба длин в зависимости от азимута.
Приняв точку 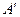 за начало прямоугольных координат и за полюс плоских полярных координат
за начало прямоугольных координат и за полюс плоских полярных координат 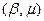 , можем написать
, можем написать
 (15)
(15)
откуда
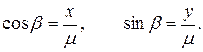 (16)
(16)
Подставим значения формулы (16) и в формулу (13) и получим уравнение центральной кривой второго порядка
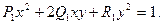
Из этого уравнения определим дискриминант
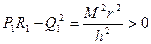
и установим, что исследуемая кривая является эллипсом. Следовательно, бесконечно малый эллипс в каждой точке на карте, являющийся изображением бесконечно малого круга на поверхности эллипсоида или шара, называется эллипсом искажений*.
Численные величины полуосей этого эллипса соответствуют величинам экстремальных масштабов, а величины двух сопряженных полудиаметров – величинам масштабов по меридианам и параллелям (рис. 2.3); при этом полудиаметр, совпадающий с направлением меридиана, повернут относительно большой полуоси эллипса на угол 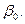
* Понятие эллипса искажений ввел в математическую картографию Тиссо.
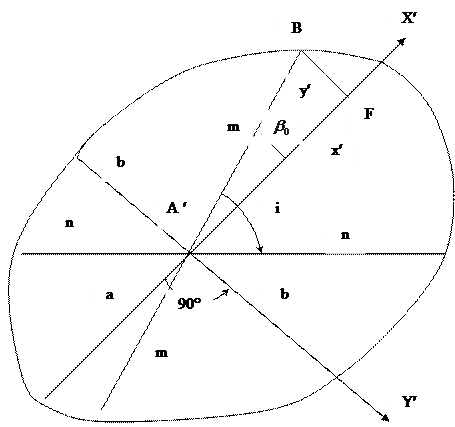
Рис 2.3. Элементы эллипса искажения
Ориентировку эллипса искажений относительно линий меридианов и параллелей определим из общего уравнения эллипса. Для этого примем, что меридианы и параллели проходят через оси 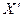 и
и 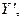 совпадающими с главными направлениями
совпадающими с главными направлениями
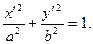
Координаты точки 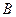 этого эллипса могут быть поучены из треугольника
этого эллипса могут быть поучены из треугольника 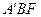 (см. рис. 2.3)
(см. рис. 2.3)
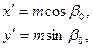
тогда
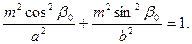
Известно, что

откуда
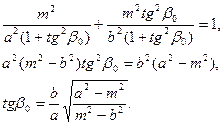 (17)
(17)
Для того, чтобы построить эллипс в заданной точке проекции, желательно знать шесть указанных выше величин: 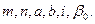
Применяя к эллипсу положения Аполлония, найдем формулы связи экстремальных масштабов с масштабами по меридианам и параллелям.
 2015-01-30
2015-01-30 2812
2812








