2015-01-30
1380
Азимут произвольного направления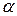 
в проекции обозначим через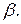 
Для определения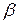 
построим на плоскости изображение элементарной сфероидической трапеции (рис. 2.1).
Найдем угол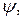 
который образует элементарный отрезок 
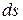с положительным направлением оси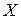 
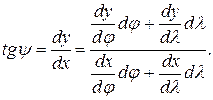
Пользуясь этой формулой, можем найти также углы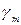 
и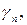 
которые образуют с положительным направлением оси 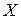меридианы и параллели (или касательные к ним).
 |
Рис. 2.1. Угол между меридианами и параллелями
Принимая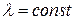 
для меридиана и 
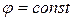для параллели, найдем
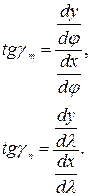
Найдем азимут элементарного отрезка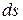
Тогда
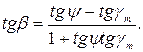
Подставим в эту формулу значения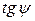 
и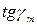 
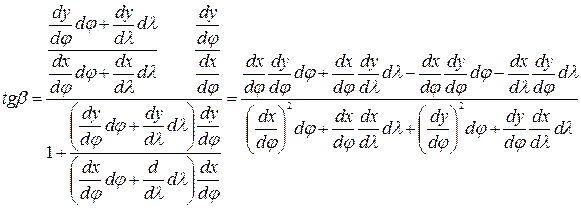
После несложных преобразований
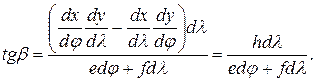
Введем вспомогательную функцию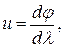 
тогда
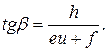(9)
Подставив в последнее уравнение из формулы (6) значение
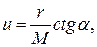
Получим
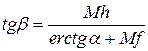(10)
Или
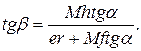(10а)
На основании рисунка 2.2 можем получить угол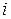 
между изображениями меридианов и параллелей
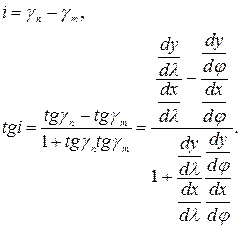
После приведения к общему знаменателю
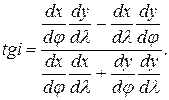
Выразив полученное выражение через коэффициенты Гаусса, получим
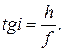
Отсюда
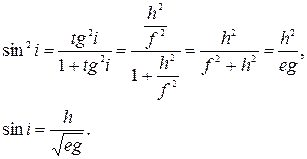(11)
Если отсчитывать угол в том же направлении, что и азимут, то значение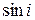 
будет положительным
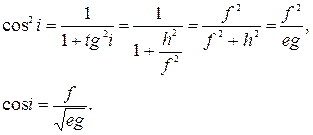
Последняя формула позволяет определить четверть, в которой находится угол 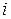: если f>0, то это первая четверть; если f<0, то – вторая; при f=0 угол i=90° и сетка становится ортогональной.
Условие ортогональности картографической сетки
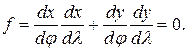
Вместо угла 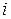в математической картографии обычно пользуются углом 
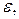который показывает уклонение угла между меридианами и параллелями от 90°, эта величина характеризует неортогональность картографической сетки
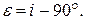
Если
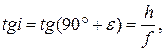
То
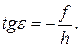(12)
