В дифференциальном исчислении решается задача: по данной функции 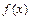 найти ее производную. Интегральное исчисление решает обратную задачу: найти функцию
найти ее производную. Интегральное исчисление решает обратную задачу: найти функцию 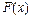 , зная ее производную.
, зная ее производную.
Определение 1. Функция 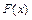 называется первообразной функции
называется первообразной функции 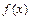 на интервале
на интервале 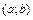 , если для любого
, если для любого 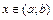 выполняется равенство
выполняется равенство 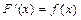 .
.
Теорема 1. Если функция 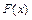 является первообразной функции
является первообразной функции 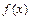 на
на 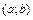 , то множество всех первообразных для
, то множество всех первообразных для 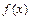 задается формулой
задается формулой 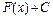 , где
, где 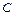 – постоянное число.
– постоянное число.
Определение 2. Множество всех первообразных функций 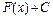 для
для 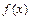 называется неопределенным интегралом о т функции
называется неопределенным интегралом о т функции 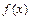 и обозначается символом
и обозначается символом 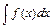 ., т.о
., т.о 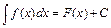 .
.
Здесь 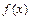 – подынтегральная функция,
– подынтегральная функция, 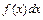 – подынтегральное выражение,
– подынтегральное выражение, 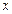 – переменная интегрирования,
– переменная интегрирования,
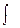 – знак неопределенного интеграла.
– знак неопределенного интеграла.
 Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
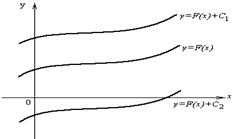
Геометрически неопределенный интеграл представляет собой семейство параллельных кривых 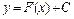 . Графикпервообразной называется интегральной кривой (см. рисунок 1).
. Графикпервообразной называется интегральной кривой (см. рисунок 1).
Всякая непрерывная на 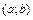 функция имеет на этом промежутке неопределенный интеграл. Результат интегрирования проверяется дифференцированием.
функция имеет на этом промежутке неопределенный интеграл. Результат интегрирования проверяется дифференцированием.
1. 2 Основные свойства неопределенного интеграла
1. Производная неопределенного интеграла равна подынтегральной функции: 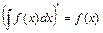 .
.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению: 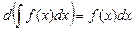 .
.
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: 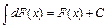 , в частности,
, в частности, 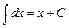 .
.
4. Постоянный множитель можно выносить за знак интеграла: 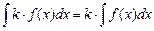 , где
, где 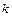 –
– 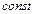 .
.
5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: 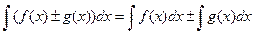 .
.
6. Если 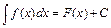 и
и 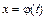 – дифференцируемая функция, то
– дифференцируемая функция, то 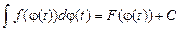 ,
,
то есть формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией, имеющей непрерывную производную.
Правила интегрирования Если 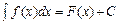 , то 1.)
, то 1.) 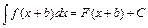 .
.
2.) 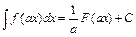 3)
3) 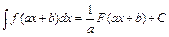 .
.
1.3 Таблица основных интегралов
1) 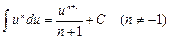 ; 2.)
; 2.) 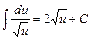 ; 3).
; 3). 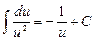 ; 4)
; 4) 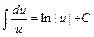 ;
;
5) 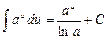 ; 6)
; 6) 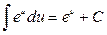 ; 7)
; 7) 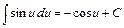 ; 8)
; 8) 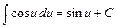 ;
;
9) 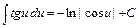 ; 10)
; 10) 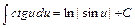 ; 11)
; 11) 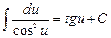 ; 12)
; 12) 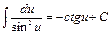 ;
;
13) 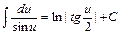 ; 14)
; 14) 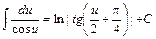 ; 15)
; 15) 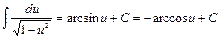 ;
;
16) 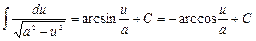 ; 17)
; 17) 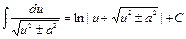 ; 18)
; 18) 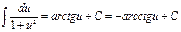 ;
;
19) 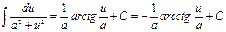 ; 20)
; 20) 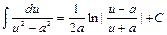 ;
;
 2015-01-30
2015-01-30 2363
2363
