Пусть 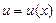 и
и 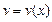 – дифференцируемые функции. Известно, что дифференциал произведения
– дифференцируемые функции. Известно, что дифференциал произведения 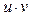 вычисляется по формуле:
вычисляется по формуле: 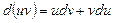 . Проинтегрируем данное равенство
. Проинтегрируем данное равенство 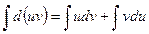 . Используя свойства интеграла, будем иметь
. Используя свойства интеграла, будем иметь 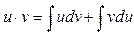 , отсюда
, отсюда 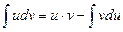 . Данная формула называется формулой интегрирования по частям. Эта формула применяется чаще всего к интегрированию выражений, которые можно представить в виде произведения двух сомножителей
. Данная формула называется формулой интегрирования по частям. Эта формула применяется чаще всего к интегрированию выражений, которые можно представить в виде произведения двух сомножителей 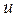 и
и 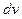 , причем за
, причем за 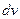 , принимают такой множитель, от которого можно найти интеграл.
, принимают такой множитель, от которого можно найти интеграл.
О сновные виды интегралов, которые берутся по частям: 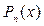 – многочлен степени
– многочлен степени 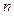 .
.
| I | 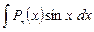
| 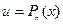
| 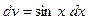
|
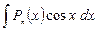
| 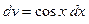
| ||
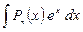
| 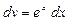
| ||
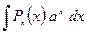
| 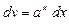
| ||
| II | 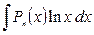
| 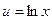
| 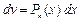
|
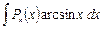
| 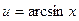
| ||
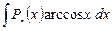
| 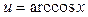
| ||
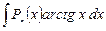
| 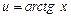
| ||
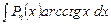
| 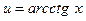
| ||
| III | 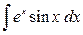
| В данных интегралах за 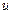 можно принять любую функцию.
Интегрируют два раза и приводят подобные интегралы. можно принять любую функцию.
Интегрируют два раза и приводят подобные интегралы.
| |
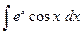
| |||
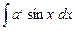
| |||
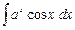
| |||
| IV | 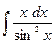
| 
| 
|
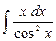
| 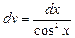
|
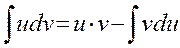 Пример. Интегрирование по частям. Найти интеграл
Пример. Интегрирование по частям. Найти интеграл 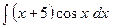 . Решение.
. Решение. 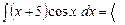
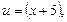
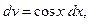 тогда
тогда 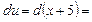
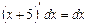 ,
, 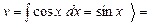
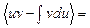
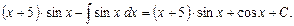
 2015-01-30
2015-01-30 459
459








