2015-01-30
572
Дано нелинейное алгебраическое уравнение f(x)=0 (1) Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
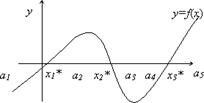Решить уравнение – это найти такое x* R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней.. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
Методы решения нелинейного уравнения (1) м ожно разделить на точные (аналитические) и приближенные (итерационные).
В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.
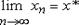В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности {x п }, такой, что.
По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |xn – x*|< ε. Члены этой последовательности xn называются последовательными приближениями к решению, или итерациями. Наперёд заданное число ε называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.
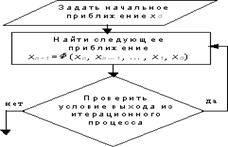
Существует различные методы нахождения приближенного решения, т.е. способы построения последовательности итераций {xn}, но все они имеют общие этапы, изображенные на рисунке.
Прежде чем использовать приближенный метод, уравнение надо исследовать его на наличие корней и уточнить, где эти корни находятся, т.е. найти интервалы изоляции корней. Интервалом изоляции корня называется отрезок, на котором корень уравнения существует и единственен. Если корней несколько, то для каждого нужно найти интервал изоляции.
