Признак сравнения: Рассмотрим два положительных числовых ряда 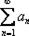 и
и 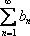 . Если известно, что ряд
. Если известно, что ряд 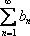 – сходится, и выполнено неравенство
– сходится, и выполнено неравенство 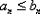 (для
(для 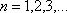 ), то ряд
), то ряд 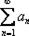 тоже сходится.
тоже сходится.
Т.е: Из сходимости ряда с большими членами следует сходимость ряда с меньшими членами.
Признак Даламбера: Рассмотрим положительный числовой ряд 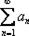 . Если существует предел отношения последующего члена к предыдущему:
. Если существует предел отношения последующего члена к предыдущему: 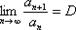 , то:
, то:
а) При 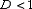 ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при 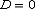 .
.
б) При 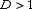 ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при 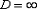 .
.
в) При 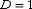 признак не дает ответа. Нужно использовать другой признак.
признак не дает ответа. Нужно использовать другой признак.
Радикальный признак Коши: Рассмотрим положительный числовой ряд 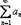 . Если есть предел:
. Если есть предел: 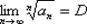 , то:
, то:
а) При 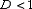 ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при 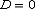 .
.
б) При 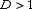 ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при 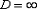 .
.
в) При 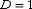 признак не дает ответа. Нужно использовать другой признак. Признак Коши является более сильным признаком, чем признак Даламбера. Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень извлекается из общего члена ряда. Интегральный признак Коши: Рассмотрим положительный числовой ряд
признак не дает ответа. Нужно использовать другой признак. Признак Коши является более сильным признаком, чем признак Даламбера. Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень извлекается из общего члена ряда. Интегральный признак Коши: Рассмотрим положительный числовой ряд 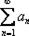 . Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.
. Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.
Знакочередующиеся ряды. Признак Лейбница.
Рассмотрим ряд 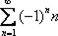 и распишем его подробнее:
и распишем его подробнее: 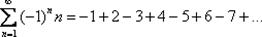 У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.
У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.
В практических примерах знакочередование членов ряда может обеспечивать не только множитель 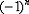 , но и:
, но и: 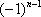 ,
, 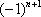 ,
, 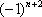 , …. Например:
, …. Например: 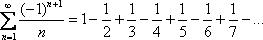
Признак Лейбница: Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.
Или, если выполнены оба условия, то ряд сходится:
1) Ряд является знакочередующимся.
2) Члены ряда убывают по модулю. То есть, 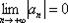
Если ряд сходится по признаку Лейбница, то также говорят, что ряд сходится условно. Если сходится и ряд, составленный из модулей: 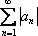 , то говорят, что ряд сходится абсолютно.
, то говорят, что ряд сходится абсолютно.
Теорема: Если ряд сходится абсолютно, то он сходится и условно.
(Обратное неверно: если ряд сходится условно, то это еще не значит, что он сходится абсолютно.)
Функциональный ряд состоит из ФУНКЦИЙ: 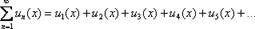 Все члены функционального ряда – это функции.
Все члены функционального ряда – это функции. 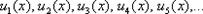
В общий член ряда помимо многочленов, факториалов и др. непременно входит буковка «икс», например:. 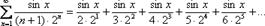 Разновидностью функционального ряда является степенной ряд.
Разновидностью функционального ряда является степенной ряд.
Степенной ряд – это ряд, в общий член 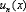 которого входят целые положительные степени независимой переменной
которого входят целые положительные степени независимой переменной  .
. 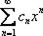 :, где
:, где  – это «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Например
– это «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Например 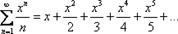 или
или 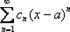 ,
, 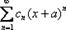 где
где  –константа. Например
–константа. Например 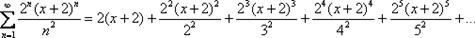 или
или 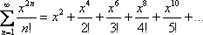 Область сходимости ряда - это множество значений «икс», при котором степенной ряд будет сходиться.
Область сходимости ряда - это множество значений «икс», при котором степенной ряд будет сходиться.
Для любого степенного ряда возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале 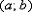 . Т.е, если мы выбираем любое значение «икс» из интервала
. Т.е, если мы выбираем любое значение «икс» из интервала 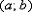 и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал
и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал 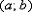 и называется интервалом сходимости степенного ряда. Радиус сходимости - половина длины интервала сходимости
и называется интервалом сходимости степенного ряда. Радиус сходимости - половина длины интервала сходимости 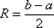
2) Степенной ряд сходится абсолютно при любом значении. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 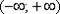 . Радиус сходимости:
. Радиус сходимости: 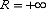
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид 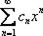 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 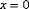 . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: 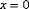 .
.
Если ряд имеет вид 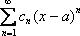 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 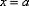 ,
,
если ряд имеет вид 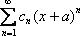 , то, понятно, – в точке «минус а».
, то, понятно, – в точке «минус а».
Радиус сходимости ряда во всех случаях, естественно, нулевой: 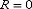 .
.
 2015-01-30
2015-01-30 2331
2331
