Теорема 2. При умножении комплексных чисел их модули перемножаются, а аргументы складываются.
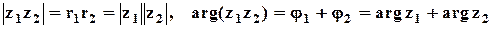 ,
,
Следствие. Если z = r(cosj + i sinj), то zn = r n (cosj + i sinj). Эта формула Муавра.
Пример 3. Вычислить (i 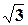 – 1)6.
– 1)6.
Решение. Запишем число – 1 + i 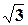 в тригонометрической форме:
в тригонометрической форме:
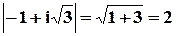 ,
, 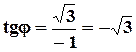 .
.
Это число изображается точкой во 2–й четверти, поэтому 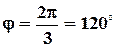 Значит
Значит 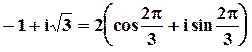 .
.
Применяем формулу Муавра: 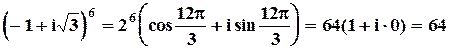 .
.
Научимся теперь извлекать корни, то есть решать уравнения zn = w, где w = | w | (cosa + i sina) – данное число, z =| z | (cosa + i sina) – неизвестная. Подставим эти выражения в уравнение:
| z | n(cosnj + i sinnj) =| w | (cosa + i sina).
Отсюда следует, что | z | n =| w |, nj = a + 2pk. Выразим теперь искомые величины |z|, j:
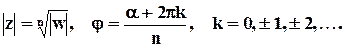
Окончательно формула для извлечения корней имеет вид:
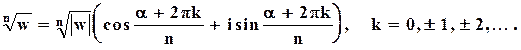
Здесь 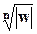 – арифметическое значение корня, то есть положительное действительное число. Среди значений
– арифметическое значение корня, то есть положительное действительное число. Среди значений 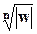 различными являются только n, соответствующие значениям k = 0, 1, 2,..., n – 1.
различными являются только n, соответствующие значениям k = 0, 1, 2,..., n – 1.
Элементарная теория погрешностей.
Математические действия над приближёнными значениями величин называются приближёнными вычислениями.
Пусть точное значение какой-либо величины равно 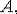 а её приближённое значение равно
а её приближённое значение равно 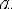 Тогда погрешность, т. е. отклонение точного значения от приближённого, равна
Тогда погрешность, т. е. отклонение точного значения от приближённого, равна 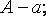
она может получиться как положительной, так и отрицательной. Эта погрешность обычно бывает точно неизвестна, поскольку неизвестно значение 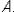 Поэтому задаются предельные погрешности
Поэтому задаются предельные погрешности 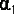 и
и 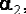 между которыми содержится истинная погрешность:
между которыми содержится истинная погрешность: 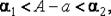 т.
т. 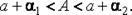
В этом случае говорят, что задана двусторонняя оценка величины 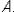 Так как задавать две предельные погрешности не всегда удобно, то часто задаётся предельная абсолютная погрешность
Так как задавать две предельные погрешности не всегда удобно, то часто задаётся предельная абсолютная погрешность 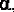 т. е. величина, большая абсолютного значения погрешности:
т. е. величина, большая абсолютного значения погрешности: 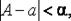 т. е.
т. е. 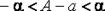 или
или 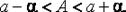
Пусть, к примеру, при измерении некоторой длины получилось ℓ = 137 см, причём можно говорить о точности до 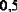 см. Это означает, что в данном случае
см. Это означает, что в данном случае 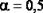 см и
см и 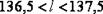 см; можно записать
см; можно записать 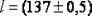 см.
см.
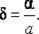 Предельная абсолютная погрешность не полностью характеризует точность измерения.. Качество измерения больше характеризуется предельной относительной погрешностью которая вычисляется по формуле
Предельная абсолютная погрешность не полностью характеризует точность измерения.. Качество измерения больше характеризуется предельной относительной погрешностью которая вычисляется по формуле
Предельная относительная погрешность безразмерна и часто выражается в процентах, причём для упрощения её значение обычно округляется в сторону увеличения.
Запись приближённых чисел, т. е. приближённых численных значений величин, производится так, чтобы сам вид записи говорил о степени точности. Обычно их записывают так, что все цифры верны, кроме последней, сомнительной, в которой допускается ошибка не больше чем на единицу. К примеру, в равенствах 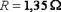 и
и 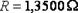 для сопротивления огромная разница, поскольку эти записи свидетельствуют, что первое вычисление производилось с точностью до
для сопротивления огромная разница, поскольку эти записи свидетельствуют, что первое вычисление производилось с точностью до 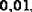 а второе − до
а второе − до 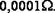
Число знаков после запятой говорит о предельной абсолютной погрешности; о предельной же относительной погрешности говорит общее число верных знаков, к которым не относятся передние нули: к примеру, числа 2,57; 1,7100; 0,015; 0,00210 имеют соответственно 3, 5, 2, 3 верных знаков. Чем больше верных знаков в числе, тем меньше предельная относительная погрешность.
Следует избегать записей вида 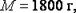 . Если вторая цифра сомнительна, то следует писать
. Если вторая цифра сомнительна, то следует писать 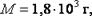 а если четвёртая − то
а если четвёртая − то 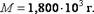
При сложении приближённых чисел в сумме берётся столько знаков после запятой, сколько их имеется у слагаемого с наибольшей абсолютной погрешностью. Если слагаемых много, то ошибки в них могут складываться и дать большую ошибку в сумме. В таких случаях рекомендуется правило лишнего знака: оставлять один лишний знак, а в ответе произвести его округление.
Например, вычислим сумму 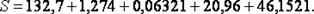 Самая большая абсолютная погрешность у первого слагаемого: она равна
Самая большая абсолютная погрешность у первого слагаемого: она равна 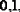 поэтому прочие слагаемые округляем до
поэтому прочие слагаемые округляем до 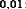
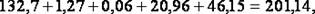 т. е.
т. е. 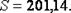
Предельная абсолютная погрешность суммы или разности нескольких величин равна сумме предельных абсолютных погрешностей этих величин.
К примеру, если две величины определены с точностью до 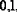 то сумма или разность этих величин определены с точностью
то сумма или разность этих величин определены с точностью 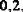 так как ошибки могут сложиться. Если же слагаемых много, то маловероятно, чтобы все ошибки сложились. В этом случае для определения погрешности суммы следует воспользоваться методами теории вероятностей, из которых вытекает, что один знак в сумме нужно округлять, как это было сделано при вычислении начиная с пяти слагаемых, а два знака − примерно с полутысячи слагаемых.
так как ошибки могут сложиться. Если же слагаемых много, то маловероятно, чтобы все ошибки сложились. В этом случае для определения погрешности суммы следует воспользоваться методами теории вероятностей, из которых вытекает, что один знак в сумме нужно округлять, как это было сделано при вычислении начиная с пяти слагаемых, а два знака − примерно с полутысячи слагаемых.
При вычитании приближённых чисел правила те же, что и при сложении, но необходимо дополнительно иметь в виду, что при вычитании близких чисел относительная точность резко ухудшается.
При умножении или делении двух приближённых чисел следует пользоваться следующим правилом: в ответечисло верных знаков надо взять равным наименьшему числу верных знаков в сомножителях или в делимом и делителе.
Важная задача теории погрешностей и метод её решения. Пусть даны приближённые значения  и
и 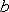 величин с точными значениями
величин с точными значениями 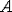 и
и 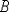 соответственно. Определим, какое из равенств
соответственно. Определим, какое из равенств 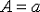 или
или 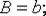 точнее. Для решения этой задачи существует следующий алгоритм.
точнее. Для решения этой задачи существует следующий алгоритм.
1. Найти приближённые значения 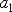 и
и 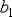 чисел
чисел 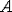 и
и 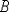 соответственно с большим числом знаков после запятой, чем у
соответственно с большим числом знаков после запятой, чем у  и
и 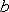
2. Найти погрешности вычислений 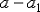 и
и 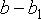 как разности между двумя приближёнными значениями чисел
как разности между двумя приближёнными значениями чисел 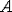 и
и 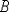 соответственно.
соответственно.
3. Определить предельные абсолютные погрешности вычислений 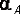 и
и 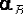 с избытком (округлить полученные значения погрешности вычислений
с избытком (округлить полученные значения погрешности вычислений 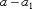 и
и 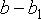 ).
).
4. Найти предельные относительные погрешности вычислений по формулам 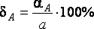 ,
, 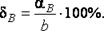
5. Сравнить предельные относительные погрешности вычисления двух чисел, сделать вывод: если 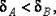 равенство
равенство 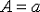 точнее равенства
точнее равенства 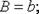 если
если 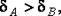 равенство
равенство 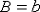 точнее равенства
точнее равенства 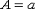
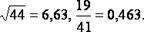 Пример. Определить, какое равенство точнее:
Пример. Определить, какое равенство точнее:
Решение. Здесь 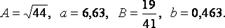
Воспользуемся алгоритмом решения задачи.
1. Найдём приближённые значения чисел 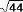 и
и 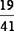 с большим числом десятичных знаков:
с большим числом десятичных знаков: 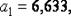
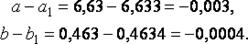
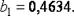
2. Найдём погрешности вычислений 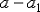 и
и 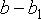 :
:
3. Определим предельные абсолютные погрешности 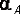 и
и 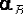 с избытком:
с избытком: 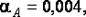
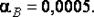
4. Найдём предельные относительные погрешности вычислений:
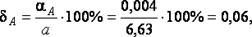
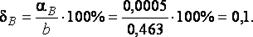
5. Поскольку 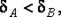 равенство
равенство 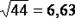 точнее равенства
точнее равенства 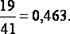
 2015-01-30
2015-01-30 1978
1978








