Введем необходимые для дальнейшего понятия. 1. Теория игр – это математическая теория конфликтных ситуаций, занимающаяся разработкой различного рода рекомендаций по принятию оптимальных решений в

1. Теория игр – это математическая теория конфликтных ситуаций, занимающаяся разработкой различного рода рекомендаций по принятию оптимальных решений в условиях конфликта.

2. Формализованная модель конфликта в теории игр называется игрой. Игра ведётся по определённым правилам, которые чётко определяют права и обязанности сторон, участвующих в игре, а также исход игры – выигрыш или проигрыш. Конфликтующие стороны называются игроками. Одна реализация игры называется партией. Выбор игроком того или иного действия называется ходом. Ходы бывают личные (игрок сознательно принимает то или иное решение) и случайные (исход игры не зависит от воли игрока).

3. Набор правил, которые определяют, какой ход игроку необходимо сделать, называется стратегией. Стратегии бывают чистыми (неслучайные решения игроков) и смешанными (стратегию можно рассматривать как случайную величину).

4. Основная задача теории игр состоит в определении оптимальных стратегий игроков.

5. Решение игры — нахождение оптимальных стратегий обоих игроков и определение цены игры Решение игры может быть найдено либо в чистых стратегиях — когда игрок должен следовать одной единственной стратегии, либо в смешанных, когда игрок должен c определенными вероятностями применять две чистые стратегии или более. Последние в этом случае называются активными.

6. Цена игры — ожидаемый выигрыш (проигрыш) игроков.

7. Теория игр занимается изучением только стратегических игр. В настоящее время наиболее простой и проработанной является теория матричных игр двух игроков с нулевой суммой. «Нулевая сумма» означает, что сумма выигрыша одного игрока равна сумме проигрыша другого.

Рассмотрим конечную игру двух игроков А и В, в которой игрок А может применить одну из 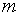стратегий

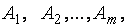
а игрок В – одну из 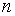стратегий

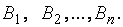
Будем предполагать везде далее, что игрок А выигрывает, а игрок B проигрывает

Пусть каждая из сторон выбрала стратеги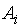и и 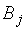соответственно ( 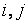фиксированы,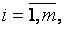 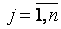). Через 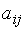обозначим исход игры (сумму выигрыша игрока А или, что то же, сумму проигрыша игрока В). Предположим, что нам известны значения 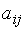при всех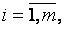 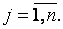Эти значения можно записать в виде матрицы, строки которой соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В:

Эту матрицу будем называть платёжной матрицей. Величина

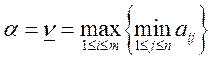
называется нижней чистой ценой игры или максимином, а величина

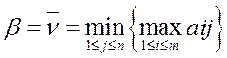
называется верхней чистой ценой игры или минимаксом.

Чистую стратегию игрока А, гарантирующую ему максимальный выигрыш, называют максиминной, а чистую стратегию игрока В, гарантирующую ему минимальный проигрыш, – минимаксной стратегией. Максиминная и минимаксная стратегии называются оптимальными стратегиями игроков А и В соответственно. Принцип, который определяет выбор игроками своих оптимальных стратегий, называют принципом минимакса.

8. В теории матричных игр доказывается, что 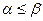. Решение матричной игры, т. е. нахождение наилучших способов её ведения, производится по–разному, в зависимости от того, 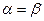или 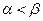. Рассмотрим эти случаи:

1). Если 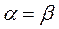то величина 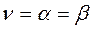называется ценой игры. Подобные игры называются играми с седловой точкой, а элемент платёжной матрицы 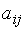, соответствующий максиминной ( 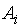) и минимаксной ( 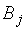) стратегиям игроков, называется седловым элементом (седловой элемент – это элемент платёжной матрицы, наименьший в своей строке и наибольший в своём столбце).

Следует отметить, что оптимальные стратегии игроков в играх с седловой точкой обладают тем свойством, что отклонение от своей оптимальной стратегии только одного игрока может лишь ухудшить положение отклонившегося.

2).Решение матричной игры с 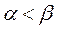находят, используя так называемые смешанные стратегии игроков – случайное чередование отдельных чистых стратегий с определённой вероятностью.

9. Критерий оптимальности стратегий. Для того, чтобы стратегии Р* и Q* были оптимальными стратегиями соответствующих игроков, а число v было ценой игры, необходимо и достаточно, чтобы выполнялись неравенства

M(P_i, Q*) ≤ v≤ М(Р*, Q_j),

где Р, (i = 1, 2,..,, m) – всевозможные чистые стратегии первого игрока, Q,; (j = 1, 2,...,n) -- всевозможные чистые стратегии второго игрока.

10. Основная теорема теории игр (теорема фон Неймана). Любая матричная игра имеет решение, то есть существуют оптимальные стратегии и цена игры

11. Связь теории матричных игр с линейным программированием

Пусть имеется произвольная матричная игра без седловой точки с платёжной матрицей 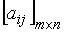. Как известно, основная задача теории игр заключается в определении оптимальных стратегий игроков и цены игры. Пусть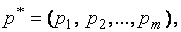 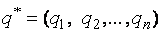− оптимальные смешанные стратегии игроков А и В соответственно.

Соотношения между 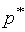и ценой игры 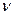можно формализовать в виде системы неравенств:

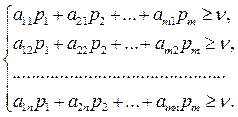(1)

причем 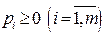и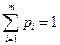

Аналогично соотношения между 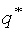и ценой игры 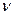можно формализовать в виде системы неравенств:

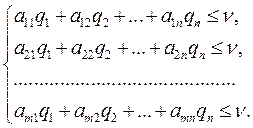(2)

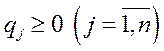и .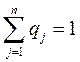

Пусть 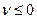. Если 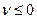всегда можно так преобразовать матричную игру, чтобы сделать её цену положительной. Положив

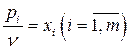и ,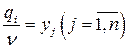

разделим неравенства системы (1) и (2) на 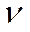. Получим следующие соотношения (см. таблицу).

Игрок А	Игрок В
Стремится максимизировать выигрыш	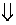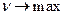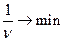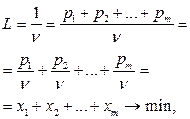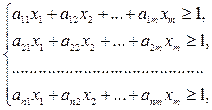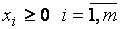Стремится минимизировать проигрыш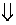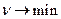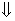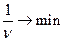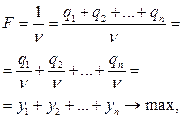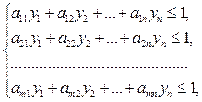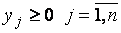

Очевидно, в левом столбце таблицы записана стандартная задача минимизации линейного программирования, а в её правом столбце − стандартная задача максимизации линейного программирования. Кроме того, представленные в таблице задачи линейного программирования образуют пару симметричных взаимодвойственных задач. Решив данные задачи линейного программирования симплекс-методом, получим и решение матричной игры:

− цену игры ;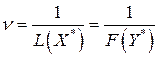

− оптимальные смешанные стратеги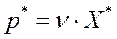и и .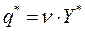

Алгоритм решения матричной игры методом
линейного программирования:

1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях, если нет, то продолжаем анализ матрицы.

2. Удаляем, если они есть, доминируемые строки и доминирующие столбцы. На их месте в оптимальных стратегиях игроков соответствующие компоненты будут равны нулю.

З. Решаем матричную игру одним из известных методов: методами линейного программирования, приближенным методом или графически (если хотя бы у одного из игроков только две чистые стратегии).

Любая матричная игра может быть сведена к паре симметричных двойственных задач линейного программирования, а значит, для отыскания оптимальных стратегий игроков и цены игры можно воспользоваться симплекс-методом.